Cálculo de la energía cinética de rotación en una rampa
En física, los objetos pueden tener ambos lineal y la energía cinética de rotación. Esto puede ocurrir cuando un objeto rueda por una rampa en lugar de deslizamiento, como parte de su energía potencial gravitatoria entra en su energía cinética lineal, y parte de ella entra en su energía cinética de rotación.
Mira la figura anterior, en el que está enfrentando a un cilindro sólido contra un cilindro hueco en una carrera por la rampa. Cada objeto tiene la misma masa. Qué cilindro va a ganar? En otras palabras, que el cilindro tendrá la mayor velocidad en la parte inferior de la rampa? Al mirar sólo al movimiento lineal, que puede manejar un problema como esto estableciendo la energía potencial igual a la energía cinética final (suponiendo que no hay fricción!) Así:
dónde m es la masa del objeto, g es la aceleración debida a la gravedad, y h es la altura en la parte superior de la rampa. Esta ecuación dejaría a resolver para la velocidad final. Dado que la masa, m, anula de ambos lados de la ecuación, la velocidad final para el movimiento lineal sin rotación es independiente de la masa.
Pero los cilindros están rodando en este caso, lo que significa que la energía potencial gravitatoria inicial se convierte ambas cosas energía cinética lineal y la energía cinética de rotación. Ahora puede escribir la ecuación como
Usted desea resolver v, así que trata de agrupar cosas juntos. Usted puede factorizar (1/2)v2 de los dos términos de la derecha:
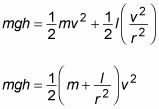
Aislar v, se obtiene el siguiente:
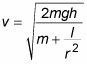
Para el cilindro hueco, el momento de inercia es igual Sr2. Para un cilindro sólido, por otro lado, el momento de inercia es igual a (1/2)Sr2. Sustituyendo yo para el cilindro hueco le da velocidad final del cilindro hueco:
Sustituyendo yo para el cilindro sólido le da la velocidad del cilindro sólido:
Ahora la respuesta se hace evidente.
1.15 veces más rápido, por lo que el cilindro sólido va a ganar.
El cilindro hueco tiene tanta masa concentrada en un gran radio que el cilindro macizo ha distribuido desde el centro de todo el camino a la radio, por lo que esta respuesta tiene sentido. Con esa gran forma masiva a cabo en el borde, el cilindro hueco no tiene que ir tan rápido como para tener la mayor cantidad de energía cinética de rotación como el cilindro sólido. De hecho, desde el momento de inercia, I, siempre depende de la masa del objeto, el término masa anula desde la parte superior e inferior de nuestra expresión anterior para la velocidad final del objeto después de que se ha rodado por la rampa. Esto significa que la velocidad final no depende de la masa en absoluto, sino solamente sobre cómo se distribuye el que la masa alrededor del eje de rotación. Para todas las formas que ruedan, se puede adivinar que uno siempre ganaría en una carrera donde ruedan por una rampa?
-
Aceleración a lo largo de rampas incluyendo la fricción -
Ya en el movimiento: la fricción cinética -
Encontrar la velocidad de un objeto en movimiento a lo largo de un plano inclinado -
Cómo la gravedad afecta a la aceleración de un objeto sobre un plano inclinado -
Cómo calcular los cambios en la energía cinética usando fuerza neta -
Cómo calcular la energía cinética de rotación
Cómo calcular la energía cinética de un objeto Puede usar la física para calcular la energía cinética de un objeto. Cuando empiece a empujar o tirar de un objeto fijo con una fuerza constante, empieza a mover si la fuerza que se ejerce es mayor que las fuerzas netas que resisten el…
Cómo calcular la energía potencial y cinética en un muelle En física, se puede examinar cómo se almacena mucha energía potencial y cinética en una primavera, cuando se comprime o estira. El trabajo que realiza la compresión o estiramiento del muelle debe ir en la energía almacenada en el resorte. Esa…
Cómo convertir la energía potencial en energía cinética Cuando un objeto se cae, su energía potencial gravitatoria se cambia a energía cinética. Usted puede usar esta relación para calcular la velocidad de descenso del objeto. Energía potencial gravitatoria de una masa m a la altura del h cerca de…
¿Cómo encontrar la velocidad de un objeto antes de la colisión En física, el principio de conservación del momento es muy útil cuando no se puede medir la velocidad con un simple cronómetro. Digamos, por ejemplo, que acepta un trabajo de consultoría de un fabricante de municiones que quiere medir la…
Cómo interpretar diagramas de energía en la física En física, la energía potencial de un objeto depende de su posición. Una roca tiene más energía potencial cuando está en la cima de una colina que cuando está rodando. En su clase de física, se le puede pedir a interpretar o dibujar un…
La energía cinética de los objetos en movimiento en problemas de física En física, se puede relacionar la masa, la velocidad de un objeto, y la energía cinética. Por ejemplo, si dos pájaros de diferentes masas están volando a la misma velocidad, se puede calcular cuánto más energía cinética utiliza el más…
Fricción cinética junto rampas Dos clases de fricción - estáticos y cinéticos - media que usted tiene que manejar los problemas de rampa donde la fricción cinética está involucrado, así como los problemas en los que interviene la fricción estática. Fricción cinética…
Física: transformar la energía entre las formas cinética y potencial La ley de conservación de la energía es una de las ideas más importantes de la ciencia. Afirma que la energía puede ser transferida o transformado pero nunca crea ni se destruye. Pero, ¿qué es esta cosa que nunca puede ser creada ni destruida?…
Ecuaciones de la física y las fórmulas Física está lleno de ecuaciones y fórmulas que tienen que ver con el movimiento angular, los motores de Carnot, fluidos, fuerzas, momentos de inercia, movimiento lineal, movimiento armónico simple, la termodinámica, y el trabajo y la…
I Física para dummies Física está lleno de ecuaciones y fórmulas que tienen que ver con el movimiento angular, los motores de Carnot, fluidos, fuerzas, momentos de inercia, movimiento lineal, movimiento armónico simple, la termodinámica, y el trabajo y la…
Almacenamiento de energía: la energía potencial Los objetos pueden tener energía en reposo simplemente por tener una fuerza de actuar en consecuencia. Por ejemplo, un objeto al final de un muelle estirado tiene energía porque cuando dejas que el objeto vaya y se acelera debido a la primavera,…
La teoría de cuerdas y la energía La teoría de cuerdas hace predicciones sobre sistemas físicos que contienen una grande cantidad de energía, embalado en un espacio muy pequeño. Las energías necesarias para las predicciones de la teoría de cuerdas son tan grandes que nunca…