Calcular el rango de un proyectil disparado con un ángulo
Si disparas un proyectil en un ángulo, puede usar la física para calcular hasta dónde va a viajar. Al calcular el movimiento de proyectiles, es necesario separar los componentes horizontal y vertical de la moción. Esto es porque la fuerza de la gravedad actúa sólo sobre el proyectil en la dirección vertical, y el componente horizontal de la velocidad de la trayectoria se mantiene uniforme.
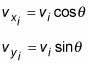
He aquí un ejemplo: Imagina que disparar una bala de cañón en un ángulo, como se muestra en la figura anterior. Dada la velocidad inicial de la bala de cañón y el ángulo en el que se rodó, se puede determinar hasta dónde va a viajar?
¿Cómo maneja el movimiento de un objeto se disparó en un ángulo? Porque siempre se puede romper el movimiento en dos dimensiones en X y y componentes, y debido a la gravedad actúa sólo en el y componente, su trabajo es fácil. Todo lo que tienes que hacer es romper la velocidad inicial en X y y componentes:
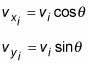
Estos componentes de velocidad son independientes, y la gravedad actúa sólo en el y dirección, lo que significa que vX está constante- única vy cambia con el tiempo, utilizando la siguiente ecuación:
vy = vyi + a, o
Si quieres saber la X y y posiciones de la bala de cañón en cualquier momento, usted puede encontrar fácilmente. Tu sabes X es
Y debido a la gravedad acelera la bala de cañón en posición vertical, esto es lo y parece que (el t2 esto es lo que da a la trayectoria de la bala de cañón en la figura de su forma parabólica):
A determinar el tiempo que tarda una bala de cañón para golpear el suelo cuando disparó hacia arriba (ignorando la resistencia del aire) así:
Conociendo el tiempo le permite encontrar el rango de los cañones en el X dirección:
Así que ahí lo tienes - ahora puedes averiguar el alcance del cañón dada la velocidad de la bala de cañón y el ángulo en el que se rodó.
He aquí un ejemplo: ¿Cuál es el rango de su cañón si tu objetivo es de 45 grados, lo que le da a su alcance máximo? Si la bala de cañón tiene una velocidad inicial de 860 m / s, la ecuación se utiliza se parece a esto:
Su rango es de 75 kilómetros, o casi 47 millas. No está mal.
-
La geometría del movimiento del proyectil -
La resistencia del aire y la velocidad vertical en problemas de física -
Encontrar la fuerza de la gravedad a lo largo de un plano inclinado -
Encontrar la velocidad de un objeto en movimiento a lo largo de un plano inclinado -
Cómo la gravedad afecta a la aceleración de un objeto sobre un plano inclinado -
Cómo masa, velocidad y radio de afectar a la fuerza centrípeta
Cómo calcular el tiempo que un proyectil está en el aire Cuando se lanza un proyectil en el aire, se puede usar la física para determinar cuánto tiempo va a permanecer en el aire. Debido a la fuerza de gravedad sólo actúa hacia abajo - es decir, en la dirección vertical - se puede tratar a los…
Cómo calcular la altura máxima de un proyectil De acuerdo con las leyes de la física, cuando un proyectil vuela en el aire, su trayectoria está determinada por la atracción gravitacional de la Tierra. Debido a la fuerza de gravedad sólo actúa hacia abajo - es decir, en la dirección…
Cómo calcular la energía cinética de un objeto Puede usar la física para calcular la energía cinética de un objeto. Cuando empiece a empujar o tirar de un objeto fijo con una fuerza constante, empieza a mover si la fuerza que se ejerce es mayor que las fuerzas netas que resisten el…
Cómo convertir la energía potencial en energía cinética Cuando un objeto se cae, su energía potencial gravitatoria se cambia a energía cinética. Usted puede usar esta relación para calcular la velocidad de descenso del objeto. Energía potencial gravitatoria de una masa m a la altura del h cerca de…
¿Cómo encontrar la velocidad de un objeto antes de la colisión En física, el principio de conservación del momento es muy útil cuando no se puede medir la velocidad con un simple cronómetro. Digamos, por ejemplo, que acepta un trabajo de consultoría de un fabricante de municiones que quiere medir la…
Los modos de exposición avanzados El canon rebel xsi digitales / de 450d Los cinco modos de exposición avanzados de la Canon EOS Digital Rebel XSi / 450D te dan más control sobre sus ajustes de la cámara que se obtiene utilizando los modos automáticos. En P, Tv, Av, y los modos M, puede ajustar la abertura (f-stop)…
Canon EOS 60D para dummies CreateThumbnail: falseLa Canon 60D es una cámara bien diseñado, con un montón de botones y diales, un monitor LCD articulado que gira y gira, una ranura para tarjetas de memoria y puertos IO. Utilice las siguientes fotos para encontrar todas…
Canon eos rebel t5 / 1200d para dummies He aquí un resumen de los botones, diales, y otros controles externos de la cámara Canon EOS Rebel T5 / 1200D. La lente se muestra en las siguientes figuras es el 18-55mm Canon EF-S IS (Estabilización de la imagen) Modelo II vendidos con el…
Canon eos 70d para dummies He aquí un resumen de los botones, diales, y otros controles externos de la cámara Canon EOS 70D. La lente se muestra en las siguientes figuras es el 18-135mm Canon EF-S IS modelo (estabilización de imagen) se vende con el cámara- otras lentes…
Canon eos rebel t6i / 750D para dummies He aquí un resumen de los botones, diales, y otros controles externos de la cámara Canon EOS Rebel T6i / 750D. La lente se muestra en las siguientes figuras es el 18-55mm Canon EF-S IS (Estabilización de la imagen) Modelo II vendidos con el…
Canon EOS Rebel XS / 1000D para dummies Todos los mandos y botones de la Canon EOS Rebel XS / 1000D están ahí para ayudar a tomar las mejores fotos posibles. Muchas funciones de la cámara son automáticos, pero se pueden hacer ajustes para afinar su toma de imagen.La siguiente vista de…
Cómo capturar la acción en el rebelde t5 canon / 1200d Para capturar tomas de acción en la Canon Rebel T5 / 1200D usted tendrá que entender la velocidad de obturación. Una velocidad de obturación rápida es la clave para la captura de un tiro de falta de definición libre de cualquier objeto en…