Encontrar la fuerza de la gravedad a lo largo de un plano inclinado
Puede usar la física para determinar la fuerza de la gravedad sobre un objeto que se mueve a lo largo de un plano inclinado. Puede romper el peso del objeto en componentes que son paralelas a y perpendicular al plano. El componente perpendicular al plano presiona el objeto en la superficie del avión. El componente del peso que actúa a lo largo del plano acelera el objeto en el suelo del avión. Aquí se encuentra el componente de gravedad que actúa a lo largo del avión cuando la fuerza vertical debida a la gravedad es Fg.
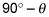
Para elaborar los componentes del paralelo peso y perpendicular al plano inclinado (la rampa en la figura), es necesario conocer la relación entre la dirección del peso total y la dirección de la rampa. La forma más sencilla de determinar esto es trabajar en el ángulo entre el peso y una línea perpendicular a la rampa. Este ángulo está etiquetado en la figura con el símbolo de theta, que es igual al ángulo de la rampa.
Hay varias maneras de utilizar la geometría para mostrar que theta es igual al ángulo de la rampa. Por ejemplo, es posible que tenga en cuenta que el ángulo entre el peso y la línea perpendicular a la rampa debe ser complementario al ángulo en la parte superior de la rampa, la cual es
Dos ángulos son complementario si se suman a los 90 grados.
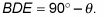
En esta figura, el ángulo de la rampa está dada por el ángulo ABC. El ángulo en la parte superior de la rampa es el complemento de esto porque los ángulos de un triángulo suman 180 grados, por lo que el ángulo de
El ángulo BCA debe ser igual al ángulo BDE porque los triángulos EBD y Abecedario son similares, por lo que se puede decir que el ángulo
Finalmente, el ángulo BCA debe ser complementario al ángulo ACF porque añaden claridad hasta 90 grados (junto con ángulo recto FCD, que formar una línea recta), para que por fin tiene su respuesta:
Si utiliza la trigonometría para proyectar el vector de pesos en las líneas perpendiculares y paralelas a la rampa (consulte la primera figura y girarlo 30 grados si al hacerlo ayuda a ver lo que está pasando), se obtiene la expresión para el componente de el peso perpendicular a la rampa ya que esto:
Y el componente del peso que es a lo largo de la rampa es la siguiente:
Porque usted sabe la fuerza, puede utilizar la segunda ley de Newton para calcular la aceleración a lo largo de la rampa:
En este punto, usted sabe que la aceleración del carro a lo largo de la rampa está dada por
Esta ecuación es válida para cualquier objeto que la gravedad acelera por una rampa, siempre y cuando la fricción no se aplica.
Calcular el rango de un proyectil disparado con un ángulo Si disparas un proyectil en un ángulo, puede usar la física para calcular hasta dónde va a viajar. Al calcular el movimiento de proyectiles, es necesario separar los componentes horizontal y vertical de la moción. Esto es porque la fuerza de la…
Cálculo de la fuerza neta y aceleración Newton dice sigmaF = mla, lo que significa que agrega todos los vectores de fuerza en conjunto para obtener la fuerza neta. Eso es lo que por lo general funciona cuando se tiene que averiguar F = mamá problemas de la física. A menudo, una serie de…
Calculando lo lejos un objeto se deslizará hacia abajo una superficie inclinada Puede usar la física para calcular qué tan lejos un objeto se deslizará hacia abajo una superficie inclinada, como una rampa. Por ejemplo, digamos que usted y sus amigos están empujando un refrigerador por una rampa en un camión de mudanzas,…
Cálculo de la fuerza necesaria para mover un objeto por una pendiente En física, cuando las fuerzas de fricción actúan sobre una superficie inclinada, tal como una rampa, el ángulo de la rampa se inclina la fuerza normal en un ángulo. Cuando se trabaja a cabo las fuerzas de fricción, es necesario tomar en cuenta…
Hacer frente a la fuerza neta Hay a menudo más de una fuerza involucrada cuando se está arrastrando una masa sobre una distancia. Basta pensar en las fuerzas de la fricción y la gravedad de un objeto sobre un plano inclinado. Por ejemplo, echar un vistazo a la figura, donde…
Encontrar la velocidad de un objeto en movimiento a lo largo de un plano inclinado En física, se puede calcular la velocidad de un objeto que se mueve a lo largo de un plano inclinado, siempre y cuando usted sabe velocidad inicial, el desplazamiento y la aceleración del objeto. Sólo tiene que conectar esta información en la…
La fuerza es un vector Fuerza, como el desplazamiento, velocidad y aceleración, es una cantidad vectorial, que es la razón por la segunda ley de Newton se escribe como sigmaF = ma. Poner en palabras, se dice que la suma vectorial de las fuerzas que actúan sobre un…
Fricción en planos inclinados En el mundo real, cuando las cosas se deslizan por las rampas, la fricción está involucrado, y la fuerza de fricción se opone al movimiento por la rampa. La fuerza de fricción es proporcional a la fuerza de la rampa que equilibra el componente…
La fricción en superficies inclinadas en problemas de física El uso de la física, se pueden aplicar las leyes de Newton del movimiento para describir cómo la fricción afecta la manera los objetos se mueven en un plano inclinado. Diagramas de cuerpo libre también son útiles para describir las fuerzas que…
Cómo la gravedad afecta a la aceleración de un objeto sobre un plano inclinado Puede usar la física para determinar cómo la gravedad afecta a la aceleración de un objeto mientras se mueve a lo largo de un plano inclinado. Cuando estás en o cerca de la superficie de la Tierra, la fuerza de la gravedad es constante. Es una…
Cómo calcular los cambios en la energía cinética usando fuerza neta En la física, si quieres encontrar el cambio en la energía cinética de un objeto, usted tiene que considerar sólo el trabajo realizado por la fuerza neta que actúa sobre el objeto. En otras palabras, convertir sólo el trabajo realizado por la…
Fricción cinética junto rampas Dos clases de fricción - estáticos y cinéticos - media que usted tiene que manejar los problemas de rampa donde la fricción cinética está involucrado, así como los problemas en los que interviene la fricción estática. Fricción cinética…