Rompiendo rampas hasta en vectores
El primer paso para trabajar con rampas de cualquier tipo es resolver las fuerzas que se está tratando, y que significa el uso de vectores. Por ejemplo, echar un vistazo a la cesta de la figura- es en un plano inclinado, listo para rodar.
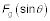
La fuerza sobre el carro es la fuerza de la gravedad, Fg = mg. Así lo rápido que va a acelerar el carro a lo largo de la rampa? Para obtener la respuesta, debe resolver la fuerza de la gravedad - no en las direcciones horizontal y vertical, sin embargo, pero a lo largo de plano inclinado de la rampa y perpendicular a ese plano.
La razón a resolver la fuerza gravitacional en estas direcciones se debe a la fuerza a lo largo del plano proporciona una aceleración del carro mientras que la fuerza perpendicular a las rampdoes no. (Cuando se inicia la introducción de la fricción en la imagen, verás que la fuerza de fricción es proporcional a la fuerza normal - es decir, que es proporcional a la fuerza con la que el objeto de bajar las pulsaciones de rampa contra la rampa.)
Ejemplo de pregunta
En la figura, ¿cuáles son las fuerzas a lo largo de la rampa y normal a la rampa?
La respuesta correcta es
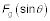
a lo largo de la rampa,
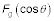
normal (perpendicular a la rampa).
Para resolver el vector Fg a lo largo de la rampa, puede empezar por averiguar el ángulo entre Fg y la rampa.
Aquí es donde viene su conocimiento de triángulos en juego. Porque usted sabe que los ángulos de un triángulo tienen que añadir hasta 180 grados, el ángulo entre Fg y el suelo es de 90 grados. La figura muestra que el ángulo de la rampa hasta el suelo es theta, para que sepa que el ángulo entre Fg y la rampa debe ser
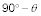
El ángulo entre Fg y la rampa es
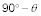
Así que lo que es el componente de Fg a lo largo de la rampa? Conociendo el ángulo entre Fg y la rampa, se puede averiguar el componente de Fg a lo largo de la rampa como de costumbre:
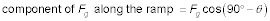
3.Aplique la siguiente ecuación:
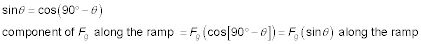
Observe que esto tiene sentido porque como theta va a 0 grados, la fuerza a lo largo de la rampa también va a cero, y como theta va a 90 grados, la fuerza a lo largo de la rampa va a Fg.
Resuelva para la fuerza normal, Fn, perpendicular a la rampa:
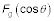
La fuerza normal, Fn, debe equilibrar exactamente la componente de la fuerza de gravedad perpendicular al plano inclinado. Aplique la siguiente ecuación:
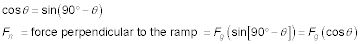
Preguntas de práctica
Supongamos que el carro en la figura tiene una masa de 1,0 kg y el ángulo theta = 30 grados. ¿Cuáles son las fuerzas que actúan sobre el carro a lo largo y normal a la rampa?
Supongamos que el carro en la figura tiene una masa de 3,0 kg y el ángulo theta = 45 grados. ¿Cuáles son las fuerzas que actúan sobre el carro a lo largo y normal a la rampa?
Usted tiene un bloque de hielo con una masa de 10.0 kg en una rampa con un ángulo de 23 grados. ¿Cuáles son las fuerzas sobre el hielo a lo largo y normal a la rampa?
Usted tiene una nevera con una masa de 1.00 x 102 kg en una rampa con un ángulo de 19 grados. ¿Cuáles son las fuerzas en el refrigerador a lo largo y normal a la rampa?
A continuación se presentan las respuestas a las preguntas de la práctica:
4,9 N a lo largo de la rampa, 8,5 N normal a la rampa
1.Usted sabe que las fuerzas en el carro son
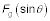
a lo largo de la rampa y
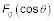
normal a la rampa.
2.Conecte los números en Fg = mg: 1,0 (9,8) = 9,8 N.
3.La fuerza a lo largo de la rampa es
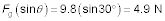
4.La fuerza normal a la rampa es
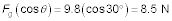
21 N a lo largo de la rampa, 21 N normal a la rampa
1.Las fuerzas en el carro son
a lo largo de la rampa y
normal a la rampa.
2.Conecte los números en Fg = mg: 3,0 (9,8) = 29 N.
3.La fuerza a lo largo de la rampa es
4.La fuerza normal a la rampa es
38 N a lo largo de la rampa, 90 N normal a la rampa
1.Las fuerzas sobre el hielo son
a lo largo de la rampa y
normal a la rampa.
2.Conecte los números en Fg = mg: 10,0 (9,8) = 98 N.
3.La fuerza a lo largo de la rampa es
4.La fuerza normal a la rampa es
320 N a lo largo de la rampa, 930 N normal a la rampa
Las fuerzas sobre el hielo son
a lo largo de la rampa y
normal a la rampa.
Conecte los números en Fg = mg: (1,00 x 102) (9,8) = 980 N.
La fuerza a lo largo de la rampa es
La fuerza normal a la rampa es
-
Aplique la función escalón unitario para el análisis de circuitos -
Aceleración y planos inclinados -
Aceleración a lo largo de rampas incluyendo la fricción -
Cálculo de la fuerza neta y aceleración -
Calculando lo lejos un objeto se deslizará hacia abajo una superficie inclinada -
Cálculo de la energía cinética de rotación en una rampa
Cálculo de la fuerza necesaria para mover un objeto por una pendiente En física, cuando las fuerzas de fricción actúan sobre una superficie inclinada, tal como una rampa, el ángulo de la rampa se inclina la fuerza normal en un ángulo. Cuando se trabaja a cabo las fuerzas de fricción, es necesario tomar en cuenta…
Hacer frente a la fuerza neta Hay a menudo más de una fuerza involucrada cuando se está arrastrando una masa sobre una distancia. Basta pensar en las fuerzas de la fricción y la gravedad de un objeto sobre un plano inclinado. Por ejemplo, echar un vistazo a la figura, donde…
Encontrar la fuerza de la gravedad a lo largo de un plano inclinado Puede usar la física para determinar la fuerza de la gravedad sobre un objeto que se mueve a lo largo de un plano inclinado. Puede romper el peso del objeto en componentes que son paralelas a y perpendicular al plano. El componente perpendicular al…
Encontrar la velocidad de un objeto en movimiento a lo largo de un plano inclinado En física, se puede calcular la velocidad de un objeto que se mueve a lo largo de un plano inclinado, siempre y cuando usted sabe velocidad inicial, el desplazamiento y la aceleración del objeto. Sólo tiene que conectar esta información en la…
La fuerza es un vector Fuerza, como el desplazamiento, velocidad y aceleración, es una cantidad vectorial, que es la razón por la segunda ley de Newton se escribe como sigmaF = ma. Poner en palabras, se dice que la suma vectorial de las fuerzas que actúan sobre un…
Fricción en planos inclinados En el mundo real, cuando las cosas se deslizan por las rampas, la fricción está involucrado, y la fuerza de fricción se opone al movimiento por la rampa. La fuerza de fricción es proporcional a la fuerza de la rampa que equilibra el componente…
La fricción en superficies inclinadas en problemas de física El uso de la física, se pueden aplicar las leyes de Newton del movimiento para describir cómo la fricción afecta la manera los objetos se mueven en un plano inclinado. Diagramas de cuerpo libre también son útiles para describir las fuerzas que…
Cómo fricción se refiere a la fuerza normal De acuerdo con las leyes de la física, la fuerza de fricción, Ffricción, siempre actúa para oponerse a la fuerza se aplica cuando intenta mover un objeto. La fricción es proporcional a la fuerza con la que un objeto empuja contra la superficie…
Cómo la gravedad afecta a la aceleración de un objeto sobre un plano inclinado Puede usar la física para determinar cómo la gravedad afecta a la aceleración de un objeto mientras se mueve a lo largo de un plano inclinado. Cuando estás en o cerca de la superficie de la Tierra, la fuerza de la gravedad es constante. Es una…
Cómo calcular los cambios en la energía cinética usando fuerza neta En la física, si quieres encontrar el cambio en la energía cinética de un objeto, usted tiene que considerar sólo el trabajo realizado por la fuerza neta que actúa sobre el objeto. En otras palabras, convertir sólo el trabajo realizado por la…
Cómo torque provoca aceleración angular En la física, cuando se gira un objeto extendido, tal como una barra, disco o cubo, que ha distribuido su masa a través del espacio, hay que tener en cuenta cuando se aplica la fuerza. Introduzca torque. Torque es una medida de la capacidad de una…
Fricción cinética junto rampas Dos clases de fricción - estáticos y cinéticos - media que usted tiene que manejar los problemas de rampa donde la fricción cinética está involucrado, así como los problemas en los que interviene la fricción estática. Fricción cinética…