Aplique la función escalón unitario para el análisis de circuitos

Los escalón unitario (Heavyside) modelos de función de la conducta de un interruptor (encendido / apagado). La función escalón unidad puede describir los cambios bruscos de corriente o voltaje en un circuito. La función escalón unitario se parece, así, un paso. Funciones escalonadas prácticas se producen a diario, al igual que cada vez que encienda los dispositivos móviles, equipos de sonido y luces de encendido y apagado. Aquí está la definición general de la función escalón unitario:

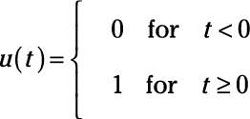
Así que esta función de paso es igual a 0 cuando el tiempo t es negativo y es igual a 1 cuando el tiempo t es 0 o positivo. Alternativamente, se puede decir que hay un salto en el valor de la función en el tiempo t = 0. gurús matemáticas llaman a esto un salto discontinuidad.

Aunque no se puede generar una función de ideales paso, puede aproximar una función escalonada. Esto es lo que una función escalonada se parece, junto con un circuito que es más o menos una función escalonada.

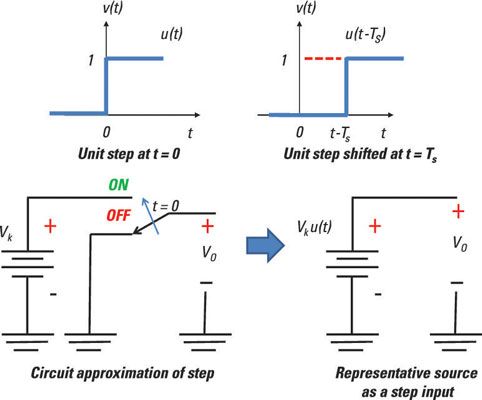
Crear una función escalón ponderada en diferido

La aproximación de circuito de la función de paso se mostró anteriormente asume que usted puede cambiar rápidamente de apagado a encendido en el momento t = 0 cuando se lanza el interruptor.

Aunque la función escalón unitario no parece hacer mucho, es una señal versátil que puede construir otras formas de onda. En un gráfico, puede hacer que el paso encoger o estirar. Puede multiplicar la función de paso u (t) por una amplitud constante V_k para producir la siguiente forma de onda:

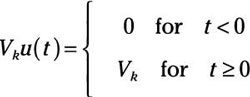
La escala o el peso de la entrada de la unidad es V_k. La amplitud V_k mide el tamaño del salto en valor de la función.

Puede mover la función escalonada en el tiempo con un cambio de T_s, que le conduce a un desplazado, de forma de onda ponderada:

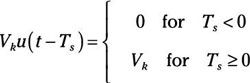
Esta ecuación dice que la función es igual a 0 antes de la hora T_s y que el valor de la función salta a V_k Tiempo después T_s. Aquí se ve la función de paso ponderado por V_k con un desplazamiento en el tiempo de T_s.

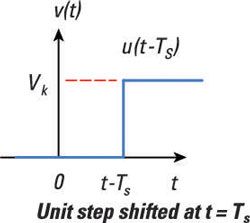
Puede agregar dos funciones escalonadas entre sí para formar una función de impulso, a medida que aprende en la siguiente sección.

Análisis de circuitos y funciones escalonadas desplazado

Funciones escalonadas pueden bailar alrededor, pero no es la fantasía tipo de giro y grito de baile. La función puede ser más grande o más pequeña y se mueven hacia la izquierda o la derecha. Usted puede agregar esas funciones escalonadas modificados para realizar funciones escalón aún más cobarde.

Por ejemplo, puede generar un pulso rectangular como una suma de dos funciones escalonadas. Este es un visual de este concepto, que muestra un pulso rectangular que se compone de la suma de dos funciones escalonadas en el tiempo.

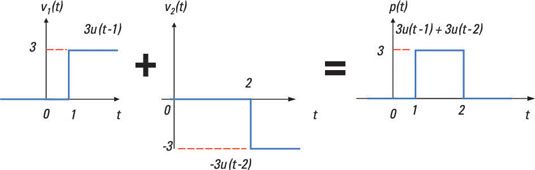
Antes de 1 segundo, el valor del pulso es 0. Entonces la amplitud del pulso salta a un valor de 3 y permanece en ese valor entre 1 y 2 segundos. El pulso vuelve entonces a 0 en el momento t = 2 segundos. Usted terminará con el impulso rectangular p (t) se describe como la suma de dos funciones escalonadas:

p (t) = 3u(t - 1) - 3u(t - 2)

Esta expresión dice que cree un pulso con una función de paso en diferido a partir de 1 segundo con una amplitud de 3 y añadirlo a otra función de paso en diferido a partir de 2 segundos con una amplitud de -3. Puedes ver el pulso en función gating para interruptores electrónicos para permitir o detener una señal del paso.

Construir una función de rampa con una función escalón

La integral de la función de paso genera una función de rampa, que consta de dos funciones multiplican entre sí:

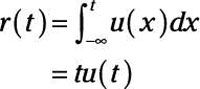
La función de tiempo tu (t) es simplemente una función de rampa con una pendiente (o fuerza) de 1, y la función escalón unidad sirve como una herramienta matemática conveniente para iniciar la rampa en el momento t = 0. Puede añadir una resistencia K a la rampa y cambiar la función de rampa en el tiempo por T_S como sigue:

v (t) = Kr (t - T_S)

La rampa no se inicia hasta T_S. Antes de que el cambio de hora T_S, la función de rampa es 0. Después de un tiempo T_S, la rampa tiene un valor igual a Kr(t - T_S).

Con funciones de rampa, puede crear funciones triangulares y diente de sierra (o formas de onda). Aquí ves una rampa de fortaleza unidad, una rampa de la fuerza K con un cambio de tiempo de 1, una forma de onda triangular, y una forma de onda de diente de sierra.

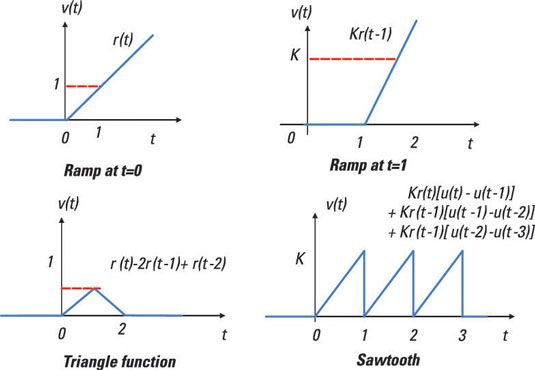
La construcción de este tipo de formas de onda de otras funciones es útil cuando se está rompiendo la entrada en trozos reconocibles y aplicando superposición.

Aquí es cómo construir la función de triángulo que se muestra en la figura, utilizando funciones de rampa:

1. Encienda una rampa con una pendiente de 1 a partir de tiempo t = 0.

2. Añadir una rampa que tiene una pendiente de -2 y comienza a las t = 1.

   A t = 1, se ve el comienzo de función a disminuir con una pendiente de -1. Pero antes de eso, la pendiente de la función (de la primera rampa) es 1- adición de una rampa con una pendiente de -2 a los primeros resultados de rampa en una rampa con una pendiente de -1.

3. Desactive la segunda rampa mediante la adición de otra rampa retardada que tiene una pendiente de 1 y comienza en el momento t = 2.

   Adición de una rampa con una pendiente de 1 trae la pendiente de nuevo a 0.

Aquí está la matemática detrás de esto:

v(t) = r(t) - 2r(t - 1) + r(t - 2)

Aquí es cómo construir una función de diente de sierra, como la que se muestra en la figura, utilizando funciones de rampa y de paso:

1. Comience con una rampa de pendiente (o fuerza) K multiplicado por un pulso rectangular de altura de la unidad.

   El pulso consta de dos funciones escalonadas. Matemáticamente, tiene una rampa con una duración de tiempo específico:

   r₁(t) = Kr(t)[u(t) - u(t - 1)]

2. Aplicar una demora de 1 a pulso rampa r₁(t) Para obtener otro pulso rampa r₂(t) Eso es el tiempo cambió.

   Aparecerá el siguiente:

   r₂(t) = Kr₁(t - 1) = Kr(t - 1) [u(t - 1) - u(t - 2)]

3. Repita el paso 2 para obtener pulsos de rampa más retardados a partir de 2, 3, 4, y así sucesivamente.

4. Sume todas las funciones para obtener el diente de sierra s_t(t).

Aquí está la función de diente de sierra:

s_t(t) = K{r(t) [u(t) - u(t - 1)] + r(t - 1) [u(t - 1) - u(t - 2)] + # 133- +}