Cómo límites trabajan con funciones
No todas las funciones se define en cada valor de X. Funciones racionales, por ejemplo, no están definidos si el denominador de la función es 0. Puede utilizar un límite (que, si existe, representa un valor que la función tiende a acercarse como la variable independiente se aproxima a un número dado) para mirar una función para ver lo que sería hacerlo si pudiera.
Para ello, se toma una mirada en el comportamiento de la función como la variable X se aproxima al valor indefinido (s). Por ejemplo, esta función no está definida para X = 3:
Puedes ver los valores de F(X) a X = 2, X = 2,9, X = 2,99, X = 2,999, y así sucesivamente. A continuación se puede ver en los valores de F(X) De nuevo desde el otro lado: X = 4, X = 3,1, X = 3,01, y así sucesivamente. Todos estos valores de F(X) están definidos, excepto para X = 3.
Para expresar un límite en símbolos, que escribes
que se lee como "el límite X enfoques c de F(X) es L." L es el límite que usted está buscando. Para el límite de una función de existir, el límite izquierdo y el límite derecho deben existir tanto y ser iguales:
LA límite izquierdo de (X) Es el valor que F(X) Se aproxima cuando X enfoques n a partir de valores de menos de c (desde la izquierda; lado de la gráfica).
LA límite de la derecha de F(X) Es el contrario- exacta es el valor que F(X) Se aproxima cuando X enfoques c a partir de valores mayor que c (desde la derecha; lado de la gráfica).
Si, y sólo si, la izquierda, límite de la mano es igual a la derecha; límite de la mano se puede decir que la función tiene un límite para el valor de c.
Matemáticamente, te dejarías F ser una función y dejar c y L ser números reales. entonces
exactamente cuando
En el lenguaje del mundo real, esta disposición significa que si usted tomó dos lápices, uno en cada mano, y comenzó a rastrear a lo largo de la gráfica de la función en la misma medida, los dos lápices tendrían que reunirse en un solo lugar en el centro con el fin de el límite exista. (La figura muestra que a pesar de que la función no está definida en X = 3, el límite existe como X enfoques 3.)
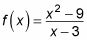
Para las funciones que son bien comunicado, los lápices siempre cumplen con el tiempo en un lugar en particular (en otras palabras, siempre existiría un límite). Sin embargo, a veces no (como se ve en la figura como X enfoques -5). El popular función escalón unitario Se define como F(X) = 0 para
y F(X) = 1 para X > 0. Si dibuja esta función, ver un salto en escalón unitario X = 0.
-
Cómo instruir a una función para salir temprano en la programación c - ¿Cómo enviar valores a las funciones de programación C
-
Evaluar una integral definida en la TI-83 Plus -
Comando Límite de TI-Nspire submenú cálculo cas -
Comparando convergentes y divergentes secuencias -
Cómo determinar los límites de secuencias con l'h & # 244-pital gobierno de
Cómo determinar si una función es continua Un gráfico de una función que es suave, sin ningún agujero, salta, o asíntotas se llama continua. Su profesor de pre-cálculo le dirá que tres cosas tienen que ser verdad para que una función sea continua en un cierto valor c en su…
Cómo calcular el límite de una función analítica Si tu profesor de pre-cálculo le pide para estimar el límite de una función analítica, puede simplemente crear un gráfico y poner el número que X es acercarse justo en el medio de ella. Luego, desde la izquierda en la misma fila, elija…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo encontrar el límite de una función gráfica Cuando se te da la gráfica de una función y su profesor de pre-cálculo le pide que encontrar el límite, usted lee los valores de la gráfica - algo que has estado haciendo desde que usted aprendió lo que era un gráfico! Si usted está buscando…
¿Cómo encontrar el límite de una función algebraica Cuando su profesor de pre-cálculo le pide que encontrar el límite de una función algebraica, usted tiene cuatro técnicas para elegir: enchufar el X valor, el factoring, racionalizar el numerador, y encontrar el mínimo común denominador.El…
¿Cómo resolver un problema de límite de plug-and-chu Algunos problemas de límite, como los problemas de plug-and-chug, son muy fáciles de resolver. Sólo tiene que conectar el número de flecha en la función de límite, y si los resultados de cálculo de un número, esa es su respuesta (pero ver la…
¿Cómo resolver los límites en el infinito con una calculadora Despejando límites en el infinito es fácil de hacer cuando se utiliza una calculadora. Por ejemplo, escribir la función debajo en el modo de gráficos de la calculadora:entonces ve a tpoder setup y establecer TblStart a 100.000 y # 8710-Tbl a…
¿Cómo resolver los límites de factoring Usted puede utilizar la técnica algebraica de factoring para resolver " verdadero " problemas de límite. Todos los métodos algebraicos implican la misma idea básica. Cuando la sustitución no funciona en la función original - por lo general a…
¿Cómo resolver límites con un sándwich de límite Cuando no se puede resolver un límite utilizando el álgebra, trate de hacer un sándwich límite. La mejor manera de entender el emparedado, o apretón, método es mirando un gráfico.El método sándwich para la solución de un límite. Funciones…
Cómo utilizar límites para determinar la continuidad Aquí usted aprenderá acerca de la continuidad para un poco, a continuación, pasar a la conexión entre la continuidad y límites, y, finalmente, pasar a la definición formal de continuidad.Definición El sentido común de la continuidadLa…
Cómo utilizar las leyes de límite en el cálculo Si conoces las leyes de límite en el cálculo, podrás encontrar los límites de todas las funciones de locos que tu profesor de pre-cálculo puede lanzar su camino. Gracias a limitar las leyes, por ejemplo, usted puede encontrar el límite de…
Límites y continuidad en pre-cálculo En matemáticas, una límite sugiere que usted está acercando a un cierto valor. Algunas funciones, tales como una función racional con una asíntota horizontal, tienen un límite como el X los valores se mueven hacia el infinito positivo o…