Cómo evaluar una integral impropia que es verticalmente infinita

Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita

integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que son horizontalmente infinita. Un integrante de este tipo contiene al menos una asíntota vertical en el área que usted está midiendo. (LA asíntota vertical es un valor de X dónde F(X) Es igual a cualquiera o -). La asíntota puede ser un límite de integración o se puede caer en alguna parte entre los dos límites de integración.

No trate de deslizar por y evaluar integrales impropias como integrales adecuadas. En la mayoría de los casos, obtendrá la respuesta equivocada!

Hay dos casos en los que usted necesita para manejar integrales impropias verticalmente infinitas.

Manipulación límites asintóticos de la integración

Suponga que desea evaluar la siguiente integral:

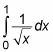
A primera vista, puede tener la tentación de evaluar esto como un integrante adecuada. Pero esta función tiene una asíntota en X = 0. La presencia de una asíntota en uno de los límites de la integración te obliga a evaluar este como una integral impropia.

1. Expresar la integral como el límite de un integrante adecuado:

   

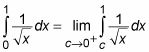
   Nótese que en este límite, c se aproxima a 0 desde la derecha - es decir, desde el lado positivo - porque esta es la dirección de aproximación desde el interior de los límites de integración. (Eso es lo que significa el pequeño signo más en el límite.)

2. Evaluar la integral:

   Esta integral es fácilmente evaluada como

   

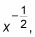
   usando la regla de la potencia:

   

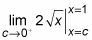
3. Evaluar el límite:

   

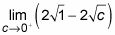
   En este punto, la sustitución directa le proporciona su respuesta final:

   = 2

Construyendo integrandos juntos discontinuos

Si una función es continua en un intervalo, también es integrable en ese intervalo. Algunas integrales que son verticalmente infinita tienen asíntotas no en los bordes, pero en algún lugar en el medio. El resultado es una integrando discontinua - es decir, una función con una discontinuidad en el intervalo que usted está tratando de integrar.

Integrandos discontinuos son los más difíciles integrales impropias de detectar - que realmente necesita saber cómo la gráfica de la función que se está integrando comporta.

Para evaluar una integral impropia de este tipo, separarla en cada asíntota en dos o más integrales. Luego de evaluar cada una de las integrales resultantes como una integral impropia.

Por ejemplo, supongamos que desea evaluar la siguiente integral:

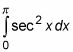
Debido a la gráfica de sec X contiene una asíntota en

la gráfica de sec² X tiene una asíntota en el mismo lugar. Por ejemplo, un gráfico de la integral impropia

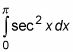
en muestra en esta figura.

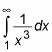
Para evaluar esta integral, dividirla en dos integrales en el valor de X donde se encuentra la asíntota:

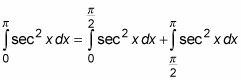
Ahora evaluar la suma de las dos integrales impropias resultantes.

Usted puede ahorrar un montón de trabajo al notar cuando dos regiones son simétricas. En este caso, la asíntota en

divide el área sombreada en dos regiones simétricas. Así que usted puede encontrar uno integral y luego duplicarlo para obtener su respuesta:

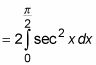
Ahora evaluar esta integral:

1. Expresar la integral como el límite de un integrante adecuado:

   

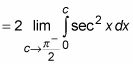
   En este caso, la asíntota vertical está en el límite superior de integración, por lo c enfoques

   

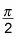
   desde la izquierda - es decir, desde el interior del intervalo en el que está midiendo el área.

2. Evaluar la integral:

   

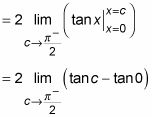
3. Evaluar el límite:

   Tenga en cuenta que

   

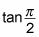
   es indefinido, porque la función de bronceado X tiene una asíntota en

   

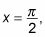
   por lo que el límite no existe (DNE). Por lo tanto, la integral que usted está tratando de evaluar también no existe porque el área que representa es infinito.