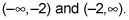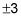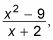Cómo graficar una función racional con numerador tiene el grado más alto

categoría Educación y lenguas / Matemáticas / Cálculo

Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales donde el numerador tiene el mayor grado en realidad no tienen asíntotas horizontales. Si el grado del numerador de una función racional es exactamente uno más que el grado de su denominador, tiene una asíntota oblicua, que se encuentra usando la división larga.

Por ejemplo, si usted desea graficar h(X), cual es

image0.jpg

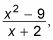
entonces usted siga estos pasos:

  1. Dibuje la asíntota vertical (s) de h(X).

    Usted encontrará sólo una asíntota vertical para esta función racional:X = -2. Y debido a que la función sólo tiene una asíntota vertical, se encuentra a sólo dos intervalos para este gráfico;

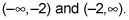
    image1.jpg

  2. Dibuje la asíntota oblicua de h(X).

    Debido a que el numerador de esta función racional tiene el mayor grado, la función tiene una asíntota oblicua. Usando la división larga, usted encuentra que la asíntota oblicua sigue la ecuación y = X - 2.

  3. Trazar la X- y y-intercepta para h(X).

    Usted encontrará que el X-intercepta son

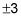
    image2.jpg

    y el y-intercepto es -9/2.

  4. Utilice los valores de prueba de su elección para determinar si el gráfico está por encima o por debajo de la asíntota oblicua.

    Observe que los intercepta convenientemente dan puntos de prueba en cada intervalo. Usted no tiene que crear sus propios puntos de prueba, pero se puede si usted realmente quiere. En el primer intervalo, el punto de prueba (-3, 0), por lo tanto, la gráfica, se encuentra por encima de la asíntota oblicua. En el segundo intervalo, los puntos de prueba (0, -9/2) y (3, 0), así como la gráfica, se encuentran debajo de la asíntota oblicua.

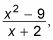
    image3.jpg

Esta figura muestra la gráfica completa de h(X).



Artículos Relacionados

Sobre el autor
Cómo determinar si una función es discontinua Cómo determinar si una función es discontinua

A medida que su profesor de pre-cálculo le dirá, funciones que no son continuas en una X valor o bien tienen un discontinuidad removible (un agujero en la gráfica de la función) o una no extraíble discontinuidad (tal como un salto o una…

¿Cómo distinguir expresiones racionales propias e impropias ¿Cómo distinguir expresiones racionales propias e impropias

Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…

Cómo evaluar una integral impropia que es verticalmente infinita Cómo evaluar una integral impropia que es verticalmente infinita

Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…

Cómo graficar una función cosecante Cómo graficar una función cosecante

Cosecante es casi exactamente el mismo que el secante porque es el recíproco de sine (a diferencia de coseno). En cualquier lugar de seno tiene un valor de 0, se ve una asíntota en el gráfico cosecante. Debido a la gráfica cruza el sine X-eje…

Cómo graficar y transformar una función exponencial Cómo graficar y transformar una función exponencial

Representación gráfica de una función exponencial es útil cuando se desea analizar visualmente la función. Si lo hace, le permite ver realmente el crecimiento o la decadencia de lo que estás tratando. La función madre básica de cualquier…

Cómo graficar una función racional cuando el numerador tiene el grado más alto Cómo graficar una función racional cuando el numerador tiene el grado más alto

Funciones racionales donde el numerador tiene el mayor grado en realidad no tienen asíntotas horizontales. En cambio, tienen asíntotas oblicuas que se encuentra utilizando la división larga.Por ejemplo, el gráfico h (X):Dibuje la asíntota…

Cómo graficar una función racional con denominador que tiene el grado más alto Cómo graficar una función racional con denominador que tiene el grado más alto

Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. En cualquier función racional donde el denominador tiene un grado…

Cómo graficar una función secante Cómo graficar una función secante

Puede representar gráficamente una función secante F(X) = Sec X mediante el uso de medidas similares a las de tangente y cotangente. Al igual que con tangente y cotangente, la gráfica de la secante tiene asíntotas. Esto es porque secante se…

Cómo graficar una función racional con numerador y el denominador de la igualdad de grados Cómo graficar una función racional con numerador y el denominador de la igualdad de grados

Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales con igualdad de grados en el numerador y el…

Cómo graficar una función tangente Cómo graficar una función tangente

La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…

Cómo graficar funciones parentales y troncos transformados Cómo graficar funciones parentales y troncos transformados

Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…

Cómo graficar polinomios Cómo graficar polinomios

Aunque puede parecer desalentador, graficar polinomios es un proceso bastante sencillo. Una vez que haya encontrado los ceros de un polinomio, puede seguir unos sencillos pasos para representarla gráficamente.Por ejemplo, si ha encontrado los ceros…

» » » » Cómo graficar una función racional con numerador tiene el grado más alto