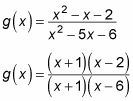Cómo determinar si una función es discontinua
A medida que su profesor de pre-cálculo le dirá, funciones que no son continuas en una X valor o bien tienen un discontinuidad removible (un agujero en la gráfica de la función) o una no extraíble discontinuidad (tal como un salto o una asíntota en el gráfico):
Si los factores de función y el término inferior cancela, la discontinuidad en el X-valor para el que el denominador es cero es desmontable, por lo que la gráfica tiene un agujero en él.
Por ejemplo, estos factores de función, como se muestra:
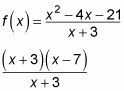
Después de la cancelación, se le deja con X - 7. Por lo tanto X + 3 = 0 (o X = -3) Es una discontinuidad removible - la gráfica tiene un agujero, como se ve en la figura a.
La gráfica de una discontinuidad removible te deja una sensación de vacío, mientras que un gráfico de una discontinuidad no extraíble deja sentir nervioso.
Si un término no cancela, la discontinuidad en este X valor correspondiente a este término para el que el denominador es cero es no extraíble, y la gráfica tiene una asíntota vertical.
Los siguientes factores de función como se muestra:
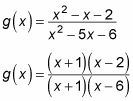
Porque el X + 1 Cancela, usted tiene una discontinuidad evitable en X = -1 (Verías un agujero en el gráfico de allí, no una asíntota). Pero el X - 6 no cancelar en el denominador, por lo que tiene una discontinuidad no extraíble en X = 6. Esta discontinuidad crea una asíntota vertical en el gráfico de X = 6. La figura b muestra la gráfica de g(X).
Sobre el autor
 Cómo graficar una función cosecante
Cómo graficar una función cosecante Cosecante es casi exactamente el mismo que el secante porque es el recíproco de sine (a diferencia de coseno). En cualquier lugar de seno tiene un valor de 0, se ve una asíntota en el gráfico cosecante. Debido a la gráfica cruza el sine X-eje…
 Cómo graficar y transformar una función exponencial
Cómo graficar y transformar una función exponencial Representación gráfica de una función exponencial es útil cuando se desea analizar visualmente la función. Si lo hace, le permite ver realmente el crecimiento o la decadencia de lo que estás tratando. La función madre básica de cualquier…
 Cómo graficar una función racional cuando el numerador tiene el grado más alto
Cómo graficar una función racional cuando el numerador tiene el grado más alto Funciones racionales donde el numerador tiene el mayor grado en realidad no tienen asíntotas horizontales. En cambio, tienen asíntotas oblicuas que se encuentra utilizando la división larga.Por ejemplo, el gráfico h (X):Dibuje la asíntota…
 Cómo graficar una función racional con denominador que tiene el grado más alto
Cómo graficar una función racional con denominador que tiene el grado más alto Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. En cualquier función racional donde el denominador tiene un grado…
 Cómo graficar una función racional con numerador tiene el grado más alto
Cómo graficar una función racional con numerador tiene el grado más alto Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales donde el numerador tiene el mayor grado en…
 Cómo graficar una función secante
Cómo graficar una función secante Puede representar gráficamente una función secante F(X) = Sec X mediante el uso de medidas similares a las de tangente y cotangente. Al igual que con tangente y cotangente, la gráfica de la secante tiene asíntotas. Esto es porque secante se…
 Cómo graficar una función racional con numerador y el denominador de la igualdad de grados
Cómo graficar una función racional con numerador y el denominador de la igualdad de grados Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales con igualdad de grados en el numerador y el…
 Cómo graficar una función tangente
Cómo graficar una función tangente La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…
 Cómo graficar funciones parentales y troncos transformados
Cómo graficar funciones parentales y troncos transformados Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…
 ¿Cómo saber cuando un derivado no existe
¿Cómo saber cuando un derivado no existe Hay tres situaciones en las que un derivado de falla de existir. La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, si no se puede trazar una línea tangente, no hay derivada - que sucede en…
 Límites y continuidad en pre-cálculo
Límites y continuidad en pre-cálculo En matemáticas, una límite sugiere que usted está acercando a un cierto valor. Algunas funciones, tales como una función racional con una asíntota horizontal, tienen un límite como el X los valores se mueven hacia el infinito positivo o…
 Encuentre la imagen especular de una función de la trigonometría en un gráfico
Encuentre la imagen especular de una función de la trigonometría en un gráfico Cuando multiplicas una función trigonométrica de un número negativo, todos los valores de salida se invierten en la señal. Los valores positivos se vuelven negativos y los valores negativos se convierten en positivos. El efecto que esta…
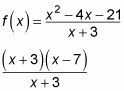
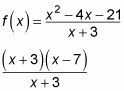 La gráfica de una discontinuidad removible te deja una sensación de vacío, mientras que un gráfico de una discontinuidad no extraíble deja sentir nervioso.
La gráfica de una discontinuidad removible te deja una sensación de vacío, mientras que un gráfico de una discontinuidad no extraíble deja sentir nervioso.