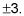Cómo calcular salidas para funciones racionales

categoría Educación y lenguas / Matemáticas / Cálculo

En pre-cálculo, se puede calcular salidas para funciones racionales. LA función racional es una función que se puede expresar como el cociente de dos polinomios, de tal manera que

image0.jpg

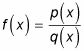
donde el grado de q(X) Es mayor que cero.

Estos son los pasos a seguir en la búsqueda de las salidas de (y en última instancia la representación gráfica) funciones racionales:

  1. Búsqueda de asíntotas verticales.

    Tener la variable en la parte inferior de una fracción es un problema, debido a que el denominador de una fracción nunca puede ser cero. Por lo general, algún valor dominio (s) de X hace que el denominador cero. Si existe una X-valor que hace que el denominador cero, pero no el numerador, entonces la gráfica tiene lo que se llama un asíntota vertical en este X-valor. Representación gráfica de la asíntota vertical primero muestra el número en el dominio donde el gráfico no puede pasar a través. La gráfica se acerca a este punto, pero nunca llega a él. Con esto en mente, ¿qué valor (s) de X puedes no conectar a la función racional?

    Las siguientes funciones son racionales:

    image1.jpg

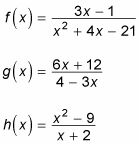
    Trate de encontrar el valor para X en el que la función no está definido. Utilice los siguientes pasos para encontrar la asíntota vertical para F(X) primero:

  1. Ajuste el denominador de la función racional igual a cero.

    por F(X), X2 + 4X - 21 = 0.

  2. Resuelva esta ecuación para X.

    Debido a que esta ecuación es una cuadrática, tratar de factorizar ella. Este cuadráticas factores a (X + 7) (X - 3) = 0. Set cada factor igual a cero para resolver. Si X + 7 = 0, X = -7. Si X - 3 = 0, X = 3. Sus dos asíntotas verticales, por lo tanto, son X = -7 Y X = 3, como se muestra en la figura.

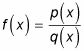
    image2.jpg

Ahora usted puede encontrar la asíntota vertical para g(X). Siga el mismo conjunto de pasos:

4 - 3X = 0

X = 4/3

Ahora usted tiene su asíntota vertical de g(X). ¡Eso fue fácil! Tiempo para hacer todo de nuevo para h(X):

X + 2 = 0

X = -2

Mantenga estas ecuaciones para las asíntotas verticales se cierran por, ya que necesitará cuando graficas más tarde.

  • Busque asíntotas horizontales.

    Para encontrar una asíntota horizontal de una función racional, que hay que buscar en el grado de los polinomios en el numerador y el denominador. los grado es la mayor potencia de la variable en la expresión polinómica. He aquí cómo usted procede:

    • Si el denominador tiene el grado más grande (como en el F(X) El ejemplo del Paso 1), la asíntota horizontal es automáticamente el X-eje, o y = 0.

    • Si el numerador y el denominador tienen el mismo grado, debe dividir los coeficientes principales (los coeficientes de los términos con los más altos grados) para encontrar la asíntota horizontal.

      Si los términos con los más altos grados no se escriben primero en el polinomio, se puede reescribir ambos polinomios de manera que los más altos grados son lo primero. Por ejemplo, se puede volver a escribir el denominador de g(X) Como -3X + 4 para que aparezca en orden descendente.

      La funcion g(X) Tiene iguales grados en la parte superior e inferior. Para encontrar la asíntota horizontal, divida los principales coeficientes de los términos de más alto grado:

      image3.jpg

      Ahora tiene su asíntota horizontal para g(X). Espera a que la ecuación para graficar!

    • Si el numerador tiene el mayor grado de exactitud uno más que el denominador, el gráfico tendrá una oblicua asymptote- consulte el Paso 3 para obtener más información sobre cómo proceder.

    • Busque asíntotas oblicuas.

      Asíntotas oblicuas no son ni horizontal ni vertical. De hecho, una asíntota ni siquiera tiene que ser una línea recta en absoluto- puede ser una ligera curva o una curva realmente complicado.

      Para encontrar una asíntota oblicua, usted tiene que utilizar la división larga de polinomios para encontrar el cociente. Usted toma el denominador de la función racional y se divide en el numerador. El cociente (despreciando el resto) le da la ecuación de la línea de su asíntota oblicua.

      Usted debe entender larga división de polinomios con el fin de completar la gráfica de una función racional con una asíntota oblicua.

      los h(X) Ejemplo de la Etapa 1 tiene una asíntota oblicua debido a que el numerador tiene el grado más alto en el polinomio. Mediante el uso de la división larga, se obtiene un cociente de X - 2. Este cociente significa la asíntota oblicua sigue la ecuación y = X - 2. Debido a que esta ecuación es de primer grado, que representa gráficamente mediante el uso de la forma pendiente-intersección. Mantenga esta asíntota oblicua en mente, porque gráfica viene la derecha para arriba!

    • Busque el X- y y-intercepta.

      La pieza final del rompecabezas es encontrar las intersecciones (donde la línea o curva cruza la X- y y-ejes) de la función racional, si existe alguno:

      • Para encontrar la y-intersección de una ecuación, ajuste X = 0. (Enchufe 0 donde vea X.) Los y-intersección de F(X) De la Etapa 1, por ejemplo, es 1/21.

      • Para encontrar la X-intersección de una ecuación, ajuste y = 0 y resolver para X.

        • Para cualquier función racional, el acceso directo a la búsqueda de la X-intercepción es establecer el numerador igual a cero y luego resolver. A veces, cuando lo hace, sin embargo, la ecuación que se obtiene es irresoluble, lo que significa que la función racional no tiene un X-intercepción.

        los X-intersección de F(X) Es 1/3.

        Esta figura muestra la gráfica de F(X).

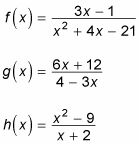
        image4.jpg

        Ahora encontrar las intersecciones para g(X) Y h(X) De la Etapa 1. Si lo hace, usted encontrará los siguientes puntos:

        • g(X) tiene un y-intercepto en 3 y una X-interceptar a -2.

        • h(X) tiene un y-intercepto en -9/2 y X-intercepta en

          image5.jpg

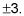
        Aquí está la gráfica de g(X):

        image6.jpg

        Aquí está la gráfica de h(X):

        image7.jpg



        Artículos Relacionados

        Sobre el autor
        ¿Cómo encontrar la ecuación de asíntotas ¿Cómo encontrar la ecuación de asíntotas

        En pre-cálculo, puede que tenga que encontrar la ecuación de asíntotas para ayudarle a esbozar las curvas de una hipérbola. Debido a hipérbolas están formados por una curva donde la diferencia de las distancias entre dos puntos es constante,…

        Cómo graficar una función cosecante Cómo graficar una función cosecante

        Cosecante es casi exactamente el mismo que el secante porque es el recíproco de sine (a diferencia de coseno). En cualquier lugar de seno tiene un valor de 0, se ve una asíntota en el gráfico cosecante. Debido a la gráfica cruza el sine X-eje…

        Cómo graficar y transformar una función exponencial Cómo graficar y transformar una función exponencial

        Representación gráfica de una función exponencial es útil cuando se desea analizar visualmente la función. Si lo hace, le permite ver realmente el crecimiento o la decadencia de lo que estás tratando. La función madre básica de cualquier…

        Cómo graficar una función racional cuando el numerador tiene el grado más alto Cómo graficar una función racional cuando el numerador tiene el grado más alto

        Funciones racionales donde el numerador tiene el mayor grado en realidad no tienen asíntotas horizontales. En cambio, tienen asíntotas oblicuas que se encuentra utilizando la división larga.Por ejemplo, el gráfico h (X):Dibuje la asíntota…

        Cómo graficar una función racional con denominador que tiene el grado más alto Cómo graficar una función racional con denominador que tiene el grado más alto

        Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. En cualquier función racional donde el denominador tiene un grado…

        Cómo graficar una función racional con numerador tiene el grado más alto Cómo graficar una función racional con numerador tiene el grado más alto

        Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales donde el numerador tiene el mayor grado en…

        Cómo graficar una función secante Cómo graficar una función secante

        Puede representar gráficamente una función secante F(X) = Sec X mediante el uso de medidas similares a las de tangente y cotangente. Al igual que con tangente y cotangente, la gráfica de la secante tiene asíntotas. Esto es porque secante se…

        Cómo graficar una función racional con numerador y el denominador de la igualdad de grados Cómo graficar una función racional con numerador y el denominador de la igualdad de grados

        Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales con igualdad de grados en el numerador y el…

        Cómo graficar una función tangente Cómo graficar una función tangente

        La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…

        Cómo graficar funciones parentales y troncos transformados Cómo graficar funciones parentales y troncos transformados

        Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…

        ¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales ¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales

        Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…

        ¿Cómo resolver los límites en el infinito mediante el uso de asíntotas horizontales ¿Cómo resolver los límites en el infinito mediante el uso de asíntotas horizontales

        Asíntotas horizontales y límites en el infinito siempre van de la mano. No se puede tener uno sin el otro. Si usted tiene una función racional comodeterminar el límite en el infinito o infinito negativo es lo mismo que encontrar la ubicación de…

        » » » » Cómo calcular salidas para funciones racionales