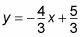¿Cómo encontrar la ecuación de asíntotas
En pre-cálculo, puede que tenga que encontrar la ecuación de asíntotas para ayudarle a esbozar las curvas de una hipérbola. Debido a hipérbolas están formados por una curva donde la diferencia de las distancias entre dos puntos es constante, las curvas se comportan de manera diferente a otras secciones cónicas. Esta cifra se compara las diferentes secciones cónicas.
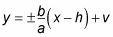
Debido a que las distancias no pueden ser negativos, la gráfica tiene asíntotas que la curva no se puede cruzar.
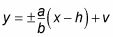
Hipérbolas son las únicas secciones cónicas con asíntotas. A pesar de parábolas e hipérbolas parecen muy similares, parábolas se forman por la distancia de un punto y la distancia a una línea siendo el mismo. Por lo tanto, parábolas no tienen asíntotas.
Algunos problemas de pre-cálculo piden que encontrar no sólo la gráfica de la hipérbola, sino también la ecuación de las líneas que determinan las asíntotas. Cuando se le preguntó a encontrar la ecuación de las asíntotas, la respuesta depende de si la hipérbola es horizontal o vertical.
Si la hipérbola es horizontal, las asíntotas son dados por la línea con la ecuación
Si la hipérbola es vertical, las asíntotas tienen la ecuación
Las fracciones b/la y la/b son las pendientes de las líneas. Ahora que sabes la pendiente de la línea y un punto (que es el centro de la hipérbola), siempre se puede escribir las ecuaciones sin tener que memorizar las dos fórmulas asíntota.
Puede encontrar la pendiente de la asíntota en este ejemplo,
siguiendo estos pasos:
Encuentra la pendiente de las asíntotas.
La hipérbola es vertical por lo que la pendiente de las asíntotas es
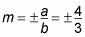
Utilice la pendiente desde el Paso 1 y el centro de la hipérbola como punto de encontrar la forma punto-pendiente de la ecuación.
Recuerde que la ecuación de una recta con pendiente m a través del punto (X1, y1) es y - y1 M =(x - x1). Por lo tanto, si la pendiente es
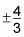
y el punto es (-1, 3), entonces la ecuación de la recta es
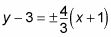
Resolver y para encontrar la ecuación en la forma pendiente-intersección.
Usted tiene que hacer cada una asíntota separado aquí.
Distribuir 4/3 a la derecha para llegar
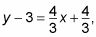
y luego agregar 3 a ambos lados para obtener
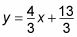
Distribuir -4/3 a la derecha para llegar
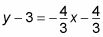
A continuación, añadir 3 a ambos lados para obtener
-
Ecuaciones lineales: cómo encontrar la pendiente, intersección y, la distancia, el punto medio -
Las secciones cónicas en pre-cálculo -
Encontrar las piezas clave de todas las hipérbolas -
Gráficas y funciones de transformación -
Cómo calcular salidas para funciones racionales -
Cómo graficar una hipérbola en 5 pasos
Cómo graficar una función cosecante Cosecante es casi exactamente el mismo que el secante porque es el recíproco de sine (a diferencia de coseno). En cualquier lugar de seno tiene un valor de 0, se ve una asíntota en el gráfico cosecante. Debido a la gráfica cruza el sine X-eje…
Cómo graficar una hipérbola Piense de una hipérbola como una mezcla de dos parábolas - cada una de ellas una imagen de espejo perfecto de la otra, cada abertura de distancia el uno del otro. Los vértices de estos parábolas están a una distancia dada de separación, y se…
Cómo graficar una función cotangente Los gráficos de los padres de tangente y cotangente son comparables, ya que ambos tienen asíntotas y X-intercepta. Las únicas diferencias se pueden ver son los valores de theta donde las asíntotas y X-se producen intersecciones. Usted puede…
Cómo graficar una función racional cuando el numerador tiene el grado más alto Funciones racionales donde el numerador tiene el mayor grado en realidad no tienen asíntotas horizontales. En cambio, tienen asíntotas oblicuas que se encuentra utilizando la división larga.Por ejemplo, el gráfico h (X):Dibuje la asíntota…
Cómo graficar una función racional con denominador que tiene el grado más alto Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. En cualquier función racional donde el denominador tiene un grado…
Cómo graficar una función racional con numerador tiene el grado más alto Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. Funciones racionales donde el numerador tiene el mayor grado en…
Cómo graficar las secciones cónicas en forma polar basado en la excentricidad Al graficar las secciones cónicas en el plano polar, utiliza ecuaciones que dependen de un valor especial conocido como excentricidad, que describe la forma general de una sección cónica. El valor de la excentricidad de una cónica puede decirle…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo identificar las cuatro secciones cónicas en forma de gráfico Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
¿Cómo trabajar con líneas en el cálculo Una línea es la función más simple que se puede representar gráficamente en el plano de coordenadas. (Líneas son importantes en el cálculo porque cuando te acercas lo suficiente en una curva, se ve y se comporta como una línea.) Esta figura…
Libro Pre-cálculo para dummies Logaritmos son simplemente otra manera de escribir exponentes. Las funciones exponenciales y logarítmicas son inversas entre sí. Para resolver y graficar funciones logarítmicas (logs), recuerde esta relación inversa y podrás registros resolver…
Funciones Gráfico tangente inversa y cotangente Las gráficas de las funciones tangente y cotangente son muy interesantes porque implican dos asíntotas horizontales. Las asíntotas ayudan con las formas de las curvas y hacer hincapié en el hecho de que algunos ángulos no funcionarán con las…