Logaritmos
Conteúdo
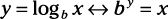
Observe que X = by > 0.
Al igual que con las funciones exponenciales, la base puede ser cualquier número positivo, excepto 1, incluyendo e. De hecho, una base de e es tan común en la ciencia y el cálculo que ingresee tiene su propio nombre especial: ln. Por lo tanto, inicie sesióneX = LnX.
Del mismo modo, inicie sesión10 es tan de uso común que a menudo se acaba de escribir como log (sin la base escrita).
Todas las funciones, incluyendo funciones trigonométricas, pueden ser descritos como par, impar, o ninguno. Saber si una función trigonométrica es par o impar puede ayudar a simplificar una expresión. Estas identidades par-impar son útiles cuando se tiene una expresión donde la variable dentro de la función trigonométrica es negativo (como -X). Las identidades par-impar son como sigue:
| pecado(-X) = -senX | csc (-X) = -cscX |
| cos (-X) = CosX | seg (-X) = SecX |
| tan (-X) = -tanX | cuna (-X) = -cotX |
Cuando la ecuación de una sección cónica no está escrito en su forma estándar, completando el cuadrado es la única manera de convertir la ecuación a su forma estándar. Los pasos del proceso son los siguientes:
Añadir / restar cualquier constante hacia el lado opuesto de la ecuación dada, lejos de todas las variables.
Factor del coeficiente principal de todos los términos en frente del conjunto de paréntesis.
Divida el coeficiente lineal restante por dos, pero sólo en su cabeza.
Cuadrar la respuesta del Paso 3 y añadir que dentro de los paréntesis.
No olvide que si usted tiene un coeficiente del paso 2, debe multiplicar el coeficiente por el número que se obtiene en este paso y añadir ese a ambos lados.
Factorizar el polinomio de segundo grado como un trinomio cuadrado perfecto.
LA hipérbola es el conjunto de todos los puntos en el plano de tal manera que la diferencia de las distancias a dos puntos fijos (la focos) Es una constante positiva. Hipérbolas siempre vienen en dos partes, y cada uno es un espejo perfecto reflejo de la otra. Hay hipérbolas horizontales y verticales, pero independientemente de cómo se abre la hipérbola, siempre se encuentran las siguientes partes:
El centro está en el punto (h, v).
La gráfica en ambos lados se acerca más y más cerca de dos líneas diagonales conocido como asíntotas. La ecuación de la hipérbola, independientemente de si es horizontal o vertical, le da dos valores: la y b. Estos ayudan a dibujar un cuadro, y cuando se dibuja las diagonales de esta casilla, encontrar las asíntotas.
Hay dos ejes de simetría:
La única que pasa a través de la vértices se llama la eje transversal. La distancia desde el centro a lo largo del eje transversal al vértice está representado por a.
El perpendicular al eje transversal a través del centro se llama eje conjugado. La distancia a lo largo del eje conjugadas desde el centro hasta el borde de la caja que determina las asíntotas está representado por b.
la y b no tienen relación- la puede ser menor que, mayor que, o igual a b.
Usted puede encontrar los focos mediante el uso de la ecuación F 2 = la2 + b2.
Para agregar o restar matrices, hay que operar en sus correspondientes elementos. En otras palabras, se añaden o se quitan la primera fila / primera columna en una matriz hacia o desde el mismo elemento exacta en otra matriz. Las dos matrices deben tener el mismo dimensiones- de otro modo, un elemento en una matriz no tendrá un elemento correspondiente en la otra.
Conceptos básicos de logaritmos 
Completando el cuadrado para las secciones cónicas Incluso identidades y pico en las funciones trigonométricas 
Las funciones exponenciales y logarítmicas utilizados en pre-cálculo Encontrar las piezas clave de todas las hipérbolas 
¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas 
Cómo completar el cuadrado Completando la plaza es muy útil cuando se le pide que resolver una ecuación cuadrática unfactorable y cuando es necesario para representar gráficamente las secciones cónicas (círculos, elipses, parábolas e hipérbolas).Sólo debe encontrar…
¿Cómo encontrar la ecuación de asíntotas En pre-cálculo, puede que tenga que encontrar la ecuación de asíntotas para ayudarle a esbozar las curvas de una hipérbola. Debido a hipérbolas están formados por una curva donde la diferencia de las distancias entre dos puntos es constante,…
Cómo graficar una hipérbola en 5 pasos Al graficar una hipérbola, se puede pensar que es una mezcla de dos parábolas - cada uno de ellos una imagen de espejo perfecto de la otra, y cada apertura de distancia el uno del otro. La definición matemática de una hipérbola es el conjunto…
Cómo graficar una hipérbola Piense de una hipérbola como una mezcla de dos parábolas - cada una de ellas una imagen de espejo perfecto de la otra, cada abertura de distancia el uno del otro. Los vértices de estos parábolas están a una distancia dada de separación, y se…
Cálculo: cómo representar gráficamente una elipse Una elipse es básicamente un círculo que ha sido aplastado, ya sea horizontal o verticalmente. Desde una perspectiva de pre-cálculo, un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada de tal manera que la…
Cómo graficar una elipse Un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada, de tal manera que la suma de las distancias desde cualquier punto de la curva a dos puntos fijos (la focos) Es una constante (siempre la misma). Una elipse es…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
¿Cómo demostrar una igualdad usando identidades pitagóricas Cuando se le preguntó para demostrar una identidad, si usted ve un negativo de una variable dentro de una función trigonométrica, se utiliza automáticamente un par / impar identidad. En primer lugar, sustituir todas las funciones…
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
¿Cómo resolver una ecuación cuadrática completando el cuadrado Puede resolver ecuaciones de segundo grado por completando el cuadrado. Completando la plaza implica la creación de un trinomio cuadrado perfecto de la ecuación de segundo grado, y luego resolver ese trinomio mediante la adopción de su raíz…
¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…