Las funciones exponenciales y logarítmicas utilizados en pre-cálculo
Las funciones exponenciales y logarítmicas van de la mano. Usted no pensaría así, a primera vista, porque las funciones exponenciales pueden parecer F(X) = 2e3X, y logarítmicas (log) pueden parecer F(X) = Ln (X2 - 3). Lo que los une es que las funciones exponenciales y funciones de registro son inversas entre sí.
Las funciones exponenciales y logarítmicas pueden tener bases que son cualquier número positivo excepto el número 1. Los casos especiales son aquellos con base 10 (logaritmos comunes) y la base e (logaritmos naturales), que van junto con sus homólogos exponenciales.
El objetivo de estas funciones es decirte qué tan grande es algo que cuando se utiliza un exponente en particular o qué tan grande de un exponente que necesita con el fin de crear un número en particular. Estas funciones se utilizan en gran medida en las ciencias y las finanzas, así estudiarlos aquí pueden pagar a lo grande en los estudios posteriores.
Usted va a trabajar con las funciones exponenciales y logarítmicas de las siguientes maneras:
La evaluación de las funciones exponenciales y de registro utilizando la regla de la función
Simplificar expresiones que involucran funciones exponenciales y de registro
Resolución de ecuaciones exponenciales utilizando reglas que implican exponentes
Resolver ecuaciones logarítmicas utilizando las leyes de los logaritmos
Representación gráfica de funciones exponenciales y logarítmicas para una mejor visión de sus poderes
La aplicación de las funciones exponenciales y logarítmicas a situaciones de la vida real
No deje que los errores comunes que viaje hasta. Éstos son algunos de los retos a los que se enfrentará al trabajar con funciones exponenciales y logarítmicas:
Usando las reglas de los exponentes en diversas operaciones correctamente
La aplicación de las leyes de los logaritmos de los denominadores de las fracciones
Recordar el orden de las operaciones al simplificar exponencial y registrar las expresiones
Comprobación de raíces extrañas al resolver ecuaciones logarítmicas
Problemas de práctica
Grafica la función exponencial: F(X) = -3X
Responder:
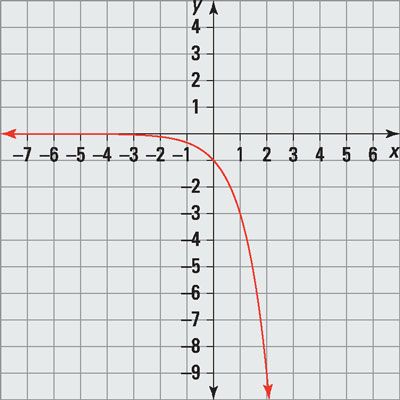
Usted encuentra el X-intercepta por despejando F(X) = 0. No hay valores de X hacen que la ecuación sea verdadera, por lo que no son X-intercepta.
Usted encuentra el y-intercepción sustituyendo por 0 X: F(0) = -30 = -1
Entonces el y-intercepción es (0, -1).
Hay una asíntota horizontal en y = 0 debido a que el límite X enfoques
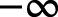
es 0. La función está disminuyendo como X enfoques
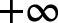
debido a que los valores de la función son cada vez más pequeños, y la función se aproxima a 0 como X enfoques
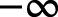
debido a la asíntota horizontal.
Resolver la ecuación exponencial para X:
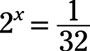
Responder: X = # 8210-5
En primer lugar, reescribir el lado derecho de la ecuación de modo que tenga la misma base que la izquierda:
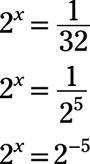
Las bases son ahora mismo, por lo que establecen los exponentes de cada lado iguales entre sí: X = -5
Cómo multiplicar exponentes Usted puede multiplicar muchas expresiones exponenciales juntos sin tener que cambiar su forma en los números grandes o pequeños que representan. Al multiplicar exponentes, el único requisito es que las bases de las expresiones exponenciales…
Conceptos básicos de logaritmos Logaritmos son simplemente otra manera de escribir exponentes. Las funciones exponenciales y logarítmicas son inversas entre sí. Para resolver y graficar funciones logarítmicas (logs), recuerde esta relación inversa y podrás registros resolver…
Fórmulas Derivados y de integración para funciones hiperbólicas Las funciones hiperbólicas son ciertas combinaciones de las funciones exponenciales eX y e-X. Estas funciones se producen con bastante frecuencia en las ecuaciones diferenciales y de ingeniería que están normalmente introducen en un curso de…
Gráficas y funciones de transformación Puede graficar funciones bastante cómodamente utilizando una calculadora gráfica, pero se le frustró el uso de esta tecnología, si usted no tiene una buena idea de lo que vas a encontrar y donde usted lo encontrará. Usted necesita tener una…
¿Cómo diferenciar las funciones exponenciales y logarítmicas Diferenciar las funciones exponenciales y logarítmicas implica reglas especiales. No se preocupe - una vez que memorizar un par de reglas, diferenciando estas funciones es un pedazo de pastel.Las funciones exponenciales: Si no puede memorizar esta…
Cómo expresar relaciones exponenciales con logaritmos Usted puede venir a través de logaritmos en su trabajo de cálculo. Un logaritmo es sólo una forma diferente de expresar una relación exponencial entre los números. Por ejemplo,Estas dos ecuaciones dicen exactamente lo mismo. Usted podría…
Cómo graficar y transformar una función exponencial Representación gráfica de una función exponencial es útil cuando se desea analizar visualmente la función. Si lo hace, le permite ver realmente el crecimiento o la decadencia de lo que estás tratando. La función madre básica de cualquier…
Cómo graficar funciones parentales y troncos transformados Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…
Cómo interpretar las gráficas de funciones Vas a ver a decenas y decenas de funciones en su estudio del cálculo, y las gráficas de estas funciones puede expresar visualmente las cosas tales como la inflación, el crecimiento demográfico y la desintegración radiactiva. A continuación se…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
¿Cómo resolver ecuaciones logarítmicas Ecuaciones logarítmicas toman diferentes formas. Como resultado de ello, antes de resolver ecuaciones que contienen los registros, es necesario estar familiarizado con los siguientes cuatro tipos de ecuaciones de registro:Tipo 1. En este tipo, la…
Libro Pre-cálculo para dummies Logaritmos son simplemente otra manera de escribir exponentes. Las funciones exponenciales y logarítmicas son inversas entre sí. Para resolver y graficar funciones logarítmicas (logs), recuerde esta relación inversa y podrás registros resolver…