Álgebra II: conceptos básicos de logaritmos y exponentes
Antes de las calculadoras de mano, los estudiantes utilizaron tablas de logaritmos (o registros) Para hacer cálculos de la física y otras clases de ciencias. Esas tablas de logaritmos de permitir que hagas multiplicación o división problemas como 456000000000 x 892658000000 o 0,00000045873 # 247- 0.0000135 simplemente agregando o restando los números de la tabla. ¿Cuáles fueron esos números? Ellos fueron los exponentes te pones un 10 para obtener ese número en particular.
¿Por exponentes? Porque cuando multiplicas números con la misma base, se agrega exponentes, y cuando se divide números con la misma base, se restan los exponentes. Aquí está un ejemplo rápido:
Multiplique 125 x 8.
Sí, usted puede hacer eso rápidamente con la mano y obtener 125 x 8 = 1.000. Usando una tabla de logaritmos, que iba a encontrar que 125 = 102.09691 y 8 = 100.90309. Añadir las dos exponentes juntos, y usted tiene 2,09691 + 0,90309 = 3. ¿Y qué potencia de 10 tiene un exponente de 3? ¿Por qué 1000, por supuesto. No todos los problemas salen tan bien, pero este ejemplo muestra por qué todavía logaritmos funcionan tan bien que hacer la multiplicación y división de números muy grandes y muy pequeños.
los leyes de los logaritmos por lo general se utilizan para ayudar a resolver ecuaciones logarítmicas. ¿Por resolver ecuaciones logarítmicas? Debido a que muchas de las ciencias utilizan fórmulas e implican cálculos que requieren trabajar con expresiones logarítmicas y exponenciales.
Las funciones exponenciales y logarítmicas están estrechamente relacionados. La inversa de una función exponencial es una función logarítmica, y viceversa. Dependiendo de lo que estás haciendo / computación, de una forma u otros trabajos mejores. Ser capaz de cambiar rápidamente la ecuación e-0.3X = 4--0,3X = Ln (4) le permite resolver para la variable X con relativa facilidad. El "ln" en la ecuación es, por supuesto, un logaritmo en la base e.
Aquí están las relaciones básicas y reglas que involucran logaritmos y exponentes:
Base 10: log10(X) = Log (X)
estos son los común logaritmos. Cuando usted no ve un subíndice 10 después de que el "registro", se asume que la base es 10.
En las calculadoras científicas, se utiliza el botón "log" para estos logaritmos comunes.
Equivalencia:
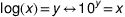
Básico e: loge(X) = Ln (X)
estos son los natural logaritmos. Cuando vea "ln", usted asume que la base es e. El valor de e es de aproximadamente 2,71828.
En las calculadoras científicas, se utiliza el botón "ln" para estos logaritmos naturales.
Equivalencia:
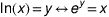
Leyes de los logaritmos: Todas las siguientes leyes se dan en términos de "log" sino que se aplican a los registros naturales, también:
Cómo dividir con el poder de cero Bueno, eso no quiere decir X tiempos cero, por lo que la respuesta no es cero. X representa algunos número- verdadero desconocido, simplemente no puede ser cero. Para entender cómo funciona esto, utilice la siguiente regla para división de…
Cómo multiplicar exponentes Usted puede multiplicar muchas expresiones exponenciales juntos sin tener que cambiar su forma en los números grandes o pequeños que representan. Al multiplicar exponentes, el único requisito es que las bases de las expresiones exponenciales…
Conceptos básicos de logaritmos Logaritmos son simplemente otra manera de escribir exponentes. Las funciones exponenciales y logarítmicas son inversas entre sí. Para resolver y graficar funciones logarítmicas (logs), recuerde esta relación inversa y podrás registros resolver…
Reglas de exponentes Los exponentes son la abreviatura para la multiplicación repetida. Las reglas para las operaciones que involucran exponentes realizar permiten cambiar las expresiones de multiplicación y división con la misma base de algo más simple. Recuerde…
Trabajar con exponentes negativos Exponentes negativos son una forma de escribir poderes de fracciones o decimales sin usar una fracción o decimal. Utiliza exponentes negativos como una manera de combinar expresiones con la misma base, si los diferentes factores están en el…
Las funciones exponenciales y logarítmicas utilizados en pre-cálculo Las funciones exponenciales y logarítmicas van de la mano. Usted no pensaría así, a primera vista, porque las funciones exponenciales pueden parecer F(X) = 2e3X, y logarítmicas (log) pueden parecer F(X) = Ln (X2 - 3). Lo que los une es que las…
¿Cómo diferenciar las funciones exponenciales y logarítmicas Diferenciar las funciones exponenciales y logarítmicas implica reglas especiales. No se preocupe - una vez que memorizar un par de reglas, diferenciando estas funciones es un pedazo de pastel.Las funciones exponenciales: Si no puede memorizar esta…
Cómo expresar relaciones exponenciales con logaritmos Usted puede venir a través de logaritmos en su trabajo de cálculo. Un logaritmo es sólo una forma diferente de expresar una relación exponencial entre los números. Por ejemplo,Estas dos ecuaciones dicen exactamente lo mismo. Usted podría…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
¿Cómo resolver ecuaciones logarítmicas Ecuaciones logarítmicas toman diferentes formas. Como resultado de ello, antes de resolver ecuaciones que contienen los registros, es necesario estar familiarizado con los siguientes cuatro tipos de ecuaciones de registro:Tipo 1. En este tipo, la…
Cómo utilizar funciones matemáticas en r En R, por supuesto, usted quiere usar más operadores simplemente básicos. R viene con un conjunto de funciones matemáticas. R contiene naturalmente todo un conjunto de funciones que te gustaría encontrar en una calculadora técnico. Todas estas…
Potencias, raíces y logaritmos para su uso en bioestadística Estas tres operaciones matemáticas - trabajar con potencias, raíces y logaritmos - están todos relacionados con la idea de multiplicación repetida. Estas funciones básicas se utilizan para ayudar a construir fórmulas más complejas.Elevar a…