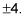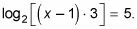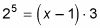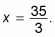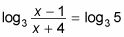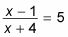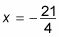¿Cómo resolver ecuaciones logarítmicas
Ecuaciones logarítmicas toman diferentes formas. Como resultado de ello, antes de resolver ecuaciones que contienen los registros, es necesario estar familiarizado con los siguientes cuatro tipos de ecuaciones de registro:
Tipo 1. En este tipo, la variable que necesita para resolver está dentro del registro, con un log en un lado de la ecuación y una constante en el otro. Gire la variable dentro del registro en una ecuación exponencial (que tiene que ver con la base, por supuesto). Por ejemplo, para resolver registro3 X = -4, Cámbielo a la ecuación exponencial 3-4 = X, o 1/81 = X.
Tipo 2. A veces la variable que necesita para resolver es la base. Si la base es lo que usted está buscando, usted todavía cambiar la ecuación a una ecuación exponencial. Si logX 16 = 2, por ejemplo, cambiar a X2 = 16, en cuyo caso X es igual a
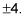
Tenga en cuenta que debido a que los registros no tienen bases negativas, que tire la negativa por la ventana y decir X = 4 solamente.
Tipo 3. En este tipo de ecuación log, la variable que necesita para resolver está dentro del registro, pero la ecuación tiene más de un registro y una constante. Puede resolver ecuaciones con más de un registro. Para resolver registro2(X - 1) registro +2 3 = 5, por ejemplo, primero combinar los dos troncos que están añadiendo en uno de registro mediante el uso de la regla del producto:
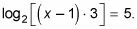
Active esta ecuación en
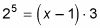
para resolverlo. La solución es
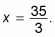
Tipo 4. Y si la variable que necesita para resolver está dentro del registro, y todos los términos de la ecuación implica registros? Si todos los términos de un problema son los registros, que tienen que tener la misma base con el fin de que usted pueda resolver la ecuación. Puede combinar todos los registros para que tenga un log de la izquierda y un tronco a la derecha, y entonces usted puede dejar el registro de ambos lados. Por ejemplo, para resolver registro3(X - 1) - registro3(X + 4) = log3 5, primero aplicar la regla del cociente para obtener
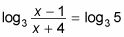
Usted puede eliminar la base de registro de 3 de ambas partes para llegar
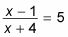
que se puede resolver fácilmente mediante el uso de técnicas de álgebra. Cuando resuelto, se obtiene
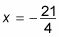
Tenga en cuenta que el número dentro de un registro nunca puede ser negativo. Al conectar esta respuesta de nuevo en parte de la ecuación original le da
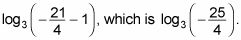
Ni siquiera tiene que mirar el resto de la ecuación. La solución a esta ecuación, por lo tanto, es en realidad el conjunto vacío: no hay solución.
Conecte siempre su respuesta a una ecuación logaritmo en la ecuación para asegurarse de obtener un número positivo en el registro (no 0 o un número negativo).
-
Cómo utilizar la función de resolver la TI-84 Plus de calculadora -
Encontrar las intersecciones de las líneas y las parábolas -
¿Cómo resolver ecuaciones lineales con división -
¿Cómo resolver ecuaciones lineales con dos multiplicación y división -
¿Cómo resolver ecuaciones lineales con la multiplicación -
Resolución de ecuaciones de valor absoluto
Resolver dos ecuaciones lineales algebraicamente Una solución de un sistema de dos ecuaciones lineales consiste en los valores de X y y que hacen ambas de las ecuaciones verdaderos - al mismo tiempo. Gráficamente, la solución es el punto donde las dos líneas se cruzan. Los dos métodos más…
Los sistemas con tres ecuaciones lineales Cuando se trabaja con sistemas de ecuaciones, puede resolver por una variable a la vez. Así, si una tercera ecuación lineal viene a lo largo (con lo cual, por supuesto, su variable z), Así, tres son multitud. Sin embargo, se puede tratar…
Los fundamentos de la resolución de ecuaciones de álgebra i Uno de los objetivos más comunes en álgebra I es resolver una ecuación. Resolver una ecuación significa para identificar el número o números que puede reemplazar la variable con hacer una declaración verdadera. Usted encontrará el factoring…
Sistemas de ecuaciones de álgebra Resolver En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una…
Los 4 pasos para resolver problemas La sola mención de problemas de palabras - o problemas de la historia, ya que están llamados a veces - es suficiente para enviar un escalofrío de terror en los huesos del estudiante promedio de matemáticas. En general, la solución de un…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
¿Cómo resolver una ecuación exponencial tomando el logaritmo de ambos lados A veces usted no puede expresar ambos lados de una ecuación exponencial como potencias de la misma base. Al hacer frente a ese problema, puede hacer que el exponente se vaya tomando el logaritmo de ambos lados. Por ejemplo, supongamos que se le…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
Resolución de ecuaciones diferenciales separables Ecuaciones diferenciales vuelven más difíciles de resolver el más enredado se vuelven. En ciertos casos, sin embargo, una ecuación que se ve enredado en realidad es fácil de separar. Las ecuaciones de este tipo se llaman ecuaciones separables…
Definición de ecuaciones diferenciales homogéneas y no homogéneas Con el fin de identificar a una ecuación diferencial no homogénea, primero tiene que sabes lo que es una ecuación diferencial homogénea se parece. También a menudo hay que resolver uno antes de poder resolver el otro.Ecuaciones diferenciales…
Preparación núcleo Praxis: cómo resolver para x y otras variables Tendrá que ser capaz de resolver para x (o cualquier variable) en el examen Praxis Core. Resolución de ecuaciones es una parte enorme de álgebra. La comprensión de cómo hacerlo te pone en una excelente posición para conquistar Praxis Core…
Praxis preparación central: sistemas de ecuaciones El examen de álgebra Praxis Core esperará que usted esté familiarizado con los sistemas de ecuaciones. Ecuaciones con dos variables pueden ser resueltos si van acompañados por una segunda ecuación con al menos una de las variables.Cuando se…