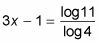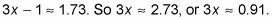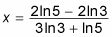¿Cómo resolver una ecuación exponencial tomando el logaritmo de ambos lados
A veces usted no puede expresar ambos lados de una ecuación exponencial como potencias de la misma base. Al hacer frente a ese problema, puede hacer que el exponente se vaya tomando el logaritmo de ambos lados. Por ejemplo, supongamos que se le pide resolver 43X - 1 = 11. Sin entero con el poder de 4 le da 11, así que tienes que usar la siguiente técnica:
Tomar el logaritmo de ambos lados.
Usted puede tomar cualquier registro que desee, pero recuerde que usted realmente necesita para resolver la ecuación con este registro, por lo que debe con sólo troncos comunes o naturales.
Utilizando el registro común en ambos lados le da ingrese 43X -1 = Log 11.
Use la regla de la potencia para desplegar el exponente.
Este paso le da (3X - 1) log 4 = log 11.
Divide ambos lados por el registro correspondiente con el fin de aislar la variable.
Usted obtiene
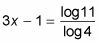
Resolver para la variable.
Tomando los registros le da
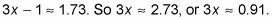
En este problema, había que utilizar la regla de la potencia en un solo lado de la ecuación porque la variable apareció en un solo lado. Cuando usted tiene que utilizar la regla de la potencia en ambos lados, las ecuaciones pueden ser un poco desordenado. Sin embargo, con persistencia, puede averiguarlo. Por ejemplo, para resolver 52 - X = 33X + 2, sigue estos pasos:
Tomar el logaritmo de ambos lados.
Al igual que con el problema anterior, se debe utilizar un registro común o un tronco natural. Si utiliza un logaritmo natural, se obtiene ln 52 - X 3 = ln3X + 2.
Use la regla de la potencia que bajar ambos exponentes.
No se olvide de incluir sus paréntesis! Usted obtiene (2 - X) ln = 5 (3X + 2) En 3.
Distribuir los registros sobre el interior de los paréntesis.
Este paso le da 2ln 5 - Xln = 3 5XEn 3 + 2ln 3.
Aislar las variables en un lado y mover todo lo demás a la otra mediante la adición o sustracción.
Ahora tiene 2ln 5 - 2ln 3 = 3XEn 3 + XEn 5.
Factorizar el X variable a partir de todos los términos adecuados.
Eso te deja con 2ln 5 - 2ln 3 = X(3LN 3 + ln 5).
Divida la cantidad en paréntesis de ambas partes para resolver de X.
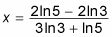
Esto equivale a aproximadamente 0.208.
Cómo graficar funciones parentales y troncos transformados Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
¿Cómo resolver ecuaciones logarítmicas Ecuaciones logarítmicas toman diferentes formas. Como resultado de ello, antes de resolver ecuaciones que contienen los registros, es necesario estar familiarizado con los siguientes cuatro tipos de ecuaciones de registro:Tipo 1. En este tipo, la…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
Cómo utilizar la diferenciación logarítmica Para diferenciar ciertas funciones, la diferenciación logarítmica es un gran atajo. Se le ahorra el dolor de cabeza de la utilización de la regla del producto o de la multiplicación de todo el asunto y luego diferenciador. Por ejemplo, digamos…
Resolución de ecuaciones diferenciales separables Ecuaciones diferenciales vuelven más difíciles de resolver el más enredado se vuelven. En ciertos casos, sin embargo, una ecuación que se ve enredado en realidad es fácil de separar. Las ecuaciones de este tipo se llaman ecuaciones separables…
Preparación ASVAB: examen de álgebra Usted se encontrará con problemas de álgebra en el ASVAB. Problemas de álgebra son ecuaciones, lo que significa que las cantidades a ambos lados del signo igual son iguales - son la misma: 2 = 2, 1 + 1 = 2, y 3 - 1 = 2. En todos estos casos, las…
Preparación ASVAB: expresiones matemáticas y ecuaciones El ASVAB se esperan que usted tenga un asimiento firme en ciertas expresiones y ecuaciones matemáticas. Matemáticas y sin expresiones y ecuaciones es como una boca de incendios sin perro- que sólo van de la mano. Entonces, ¿cuál es la…
Preparación ASVAB: cómo resolver ecuaciones cuadráticas Ecuaciones cuadráticas probablemente aparecerá en la ASVAB.A ecuación cuadrática es una ecuación algebraica en la que el desconocido se eleva a un exponente no superior a 2, como en X2. Pueden ser (grados o varios de dificultad entre los dos)…
Militar aptitud de vuelo: operaciones matemáticas para resolver para x La Prueba de Aptitud Vuelo militar podría hacer preguntas que involucran el uso de operaciones matemáticas o expresiones algebraicas. Un expresión algebraica es una colección de números y variables. Usted puede resolver expresiones algebraicas…
Militar prueba de aptitud de vuelo: álgebra básica Antes de tomar el vuelo de prueba de aptitud militar, una materia que debe revisar es el álgebra básica. Álgebra es un tema divertido en el que las letras representan las variables, y su papel es el de averiguar exactamente lo que significa que…
Preparación núcleo Praxis: cómo resolver para x y otras variables Tendrá que ser capaz de resolver para x (o cualquier variable) en el examen Praxis Core. Resolución de ecuaciones es una parte enorme de álgebra. La comprensión de cómo hacerlo te pone en una excelente posición para conquistar Praxis Core…