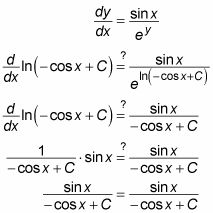Resolución de ecuaciones diferenciales separables
Ecuaciones diferenciales vuelven más difíciles de resolver el más enredado se vuelven. En ciertos casos, sin embargo, una ecuación que se ve enredado en realidad es fácil de separar. Las ecuaciones de este tipo se llaman ecuaciones separables (o ecuaciones autónomas), Y encajan en la forma siguiente:
Ecuaciones separables son relativamente fáciles de resolver. Por ejemplo, supongamos que desea resolver el siguiente problema:
Usted puede pensar en el símbolo
como una fracción y aislar el X y y términos de esta ecuación en lados opuestos del signo igual:
ey dy = Sen X dx
Ahora integrar ambos lados:
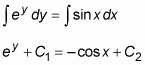
En un sentido importante, el paso anterior es cuestionable debido a la variable de integración es diferente en cada lado del signo igual. Usted puede pensar " n problema, todo es la integración "! Pero imagínese si se trató de dividir a un lado de una ecuación por 2 y el otro por 3, y luego se echó a reír apagado con "! Es toda división " Claramente, usted tendría un problema. La buena noticia, sin embargo, es que la integración de ambos lados por diferentes variables realmente produce la respuesta correcta.
C1 y C2 son las dos constantes, por lo que puede utilizar la ecuación C = C2 - C1 para simplificar la ecuación:
ey = -cos X + C
A continuación, utilice un registro natural para deshacer el exponente y, a continuación, simplificar:
ln e y = Ln (-cos X + C)
y = Ln (-cos X + C)
Para comprobar esta solución, sustituir este valor por y en ambos lados de la ecuación original:
-
¿Cómo resolver ecuaciones lineales con división -
¿Cómo resolver ecuaciones lineales con la multiplicación -
Resolución de ecuaciones de valor absoluto -
Resolver dos ecuaciones lineales algebraicamente -
Los fundamentos de la resolución de ecuaciones de álgebra i -
Ecuaciones diferenciales libro para los maniquíes
¿Cómo decirle a una ecuación diferencial de otro Antes de que pueda resolver una ecuación diferencial, lo que necesita saber de qué tipo es. Hay varios tipos diferentes de ecuaciones, incluyendo lineal, separable, exacta y homogénea, y no homogénea.Ecuaciones diferenciales lineales tratan…
Sistemas de ecuaciones de álgebra Resolver En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una…
Comprobación de soluciones de ecuaciones diferenciales Incluso si usted no sabe cómo encontrar una solución a una ecuación diferencial, siempre se puede comprobar si una propuesta de solución funciona. Esto es simplemente una cuestión de conectar el valor propuesto de la variable dependiente en…
Ecuaciones diferenciales para los maniquíes La clasificación más común de ecuaciones diferenciales se basa en el orden. El orden de una ecuación diferencial, simplemente es el fin de su más alta derivada. Usted puede tener las ecuaciones diferenciales de primera, segunda, y de orden…
Distinguir entre las ecuaciones diferenciales lineales, separables y exactas Se puede distinguir entre las ecuaciones diferenciales lineales, separables y exactas si usted sabe qué buscar. Tenga en cuenta que puede que tenga que reorganizar una ecuación para identificarlo.Ecuaciones diferenciales lineales involucrar sólo…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
¿Cómo resolver una ecuación exponencial tomando el logaritmo de ambos lados A veces usted no puede expresar ambos lados de una ecuación exponencial como potencias de la misma base. Al hacer frente a ese problema, puede hacer que el exponente se vaya tomando el logaritmo de ambos lados. Por ejemplo, supongamos que se le…
Resolución de ecuaciones diferenciales usando un factor de integración Un método inteligente para resolver ecuaciones diferenciales (ED) es en la forma de una ecuación lineal de primer orden. Este método implica multiplicar toda la ecuación por una la integración de factor. Una ecuación lineal de primer orden…
Definición de ecuaciones diferenciales homogéneas y no homogéneas Con el fin de identificar a una ecuación diferencial no homogénea, primero tiene que sabes lo que es una ecuación diferencial homogénea se parece. También a menudo hay que resolver uno antes de poder resolver el otro.Ecuaciones diferenciales…
Preparación ASVAB: expresiones matemáticas y ecuaciones El ASVAB se esperan que usted tenga un asimiento firme en ciertas expresiones y ecuaciones matemáticas. Matemáticas y sin expresiones y ecuaciones es como una boca de incendios sin perro- que sólo van de la mano. Entonces, ¿cuál es la…
Preparación núcleo Praxis: cómo resolver para x y otras variables Tendrá que ser capaz de resolver para x (o cualquier variable) en el examen Praxis Core. Resolución de ecuaciones es una parte enorme de álgebra. La comprensión de cómo hacerlo te pone en una excelente posición para conquistar Praxis Core…
Praxis preparación central: sistemas de ecuaciones El examen de álgebra Praxis Core esperará que usted esté familiarizado con los sistemas de ecuaciones. Ecuaciones con dos variables pueden ser resueltos si van acompañados por una segunda ecuación con al menos una de las variables.Cuando se…