Resolver dos ecuaciones lineales algebraicamente

Una solución de un sistema de dos ecuaciones lineales consiste en los valores de X

y y que hacen ambas de las ecuaciones verdaderos - al mismo tiempo. Gráficamente, la solución es el punto donde las dos líneas se cruzan. Los dos métodos más frecuentemente utilizados para sistemas de ecuaciones lineales resolver son la eliminación y sustitución:

• Eliminación (también llamado complemento de resta): Este método consiste en la adición de las dos ecuaciones juntos - o múltiplos de las dos ecuaciones - de modo que en la suma, el coeficiente de una de las variables se convierte en 0. esa variable se retira (se elimina), para que pueda resolver la otra variable. Luego de conectar la solución de nuevo en una de las ecuaciones originales y resolver para la variable que eliminado.

• Sustitución: Este método tiene que fijar una de las ecuaciones igual a X o y. A continuación, puede sustituir el equivalente de la variable de una ecuación para esa variable en la otra ecuación. Se termina con una sola variable de ecuación, que se puede resolver. A continuación, conecte la respuesta a una de las ecuaciones originales y resuelve para la otra variable.

Puede utilizar cualquiera de los métodos para resolver sistemas lineales, y elegir uno sobre el otro, si un método parece funcionar mejor en un sistema en particular (sustitución funciona mejor si el coeficiente en una de las variables es 1 o -1). Los siguientes ejemplos muestran el mismo sistema de ecuaciones resuelve utilizando ambos métodos.

Ejemplos de preguntas

1. Utilice la eliminación de resolver para la solución común en las dos ecuaciones: X + 3y = 4 y 2X + 5y = 5.

   X= -5, y= 3. Multiplica cada término de la primera ecuación por -2 (se obtiene -2X - 6y = -8) Y luego añadir los términos en las dos ecuaciones juntos.

   Usted elige el número -2 como multiplicador porque hace que el coeficiente de la X plazo en la primera ecuación igual a -2, mientras que el coeficiente de X en la segunda ecuación es 2. Los números de -2 y 2 son opuestos, por lo que la adición de las ecuaciones juntos elimina la X término:

   

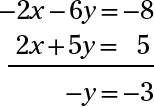
   Ahora resolver -y = -3 Para y, y se obtiene y = 3. Ponga 3 por y en la primera ecuación original, y usted tiene X + 3 (3) = 4- X + 9 = 4- X = -5. La solución es X = -5, y = 3, también escrito como el par ordenado (-5, 3). También puede resolver la X-valor al poner el 3 en la segunda ecuación - se obtiene el mismo resultado.

2. Utilice sustitución para resolver para la solución común en las dos ecuaciones: X + 3y = 4 y 2X + 5y = 5.

   X = -5, y = 3.Para utilizar la sustitución, seleccione una variable en una de las ecuaciones con un coeficiente de 1 o -1. La única variable que califica en este sistema es X en la primera ecuación. Resolver X en términos de y en esa ecuación. Usted obtiene X = 4 - 3y.

   Sustituya que equivale a X en la segunda ecuación. La segunda ecuación se convierte en 2 (4 - 3y) + 5y = 5. Resolver esta ecuación para y: 8 - 6y + 5y = 5 8 - y = 5 -y = -3- y = 3. Esa respuesta debe parecer familiar. Sustituir al 3 en X + 3y = 4 para obtener X: X + 3 (3) = 4- X + 9 = 4- X = -5.

Preguntas de práctica

1. Resuelve para la solución común en las dos ecuaciones: 5X - 3y = 7 y 2X + 3y = 7.

2. Resuelve para la solución común en las dos ecuaciones: 8X - 3y = 41 y 3X + 2y = 6.

3. Resuelve para la solución común en las dos ecuaciones: 4X + 5y = 11 y y = 2X + 5.

A continuación se presentan las respuestas a las preguntas de la práctica:

1. La respuesta es X= 2, y = 1.

   Los coeficientes de la y términos son opuestos el uno del otro, por lo que cuando se agrega las dos ecuaciones juntas, se obtiene 7X = 14- X = 2. Vuelva a colocar la X con 2 en la primera ecuación: 5 (2) - 3y = 7- 10-3y = 7, -3y = -3- y = 1.

2. La respuesta es X= 4, y = -3.

   Multiplique los términos en la primera ecuación por 2 y los términos de la segunda ecuación por 3. Como resultado, se termina añadiendo -6y y 6y juntos, lo que elimina la y términos cuando se suman las dos ecuaciones. Usted obtiene 25X = 100- X = 4. Vuelva a colocar la X con 4 en la segunda ecuación: 3 (4) + 2y = 12 + 2 6-y = 6- 2y = -6- y = -3.

3. La respuesta es X= -1, y = 3.

   La segunda ecuación se resuelve para ya y. Sustituya el equivalente de y de la segunda ecuación en la primera ecuación para obtener 4X + 5 (2X + 5) = 11. Distribuir y simplificar: 4X + 10X + 25 = 11- 14X + 25 = 11- 14X = -14- X = -1. Reemplace la X con -1 en la segunda ecuación: y 2 = (-1) + 5 = 3.