¿Cómo resolver sistemas lineales

Cuando a resolver sistemas con dos variables y por lo tanto dos ecuaciones, las ecuaciones pueden ser lineales o no lineales. Los sistemas lineales se suelen expresar en la forma Ax + By = C, donde A, B y C son números reales.

Cuando la solución de sistemas lineales, tiene dos métodos a su disposición, y que uno elige depende del problema:

• Si el coeficiente de cualquier variable es 1, lo que significa que usted puede solucionar fácilmente en términos de la otra variable, entonces la sustitución es una muy buena apuesta. Si utiliza este método, entonces no importa cómo cada ecuación se establezca.

• Si todos los coeficientes son distintos de 1 nada, entonces usted puede utilizar la eliminación, pero sólo si las ecuaciones se pueden sumar a hacer una de las variables desaparecen. Sin embargo, si utiliza este método, asegúrese de que todas las variables y la línea de la igualdad de registro entre sí antes de añadir las ecuaciones juntos.

Con el método de sustitución

en el método de sustitución, utiliza una ecuación para resolver una variable y luego sustituir esa expresión en la otra ecuación para resolver la otra variable. Busque una variable con un coeficiente de 1 # 133- así es como usted sabrá por dónde empezar. Si el coeficiente de una variable es 1, entonces esa es la variable que debe resolver porque la solución para esa variable será únicamente implicaría sumar o restar términos con el fin de mover todo al otro lado del signo igual. De esa manera, usted no tendrá que dividir por el coeficiente cuando se está resolviendo, lo que significa que no tendrá ningún fracciones.

Por ejemplo, supongamos que usted está la gestión de un teatro, y lo que necesita saber cuántos adultos y niños están en la asistencia a un espectáculo. El auditorio está agotado y contiene una mezcla de adultos y niños. Los boletos cuestan $ 23.00 por adulto y $ 15.00 por niño. Si el auditorio tiene capacidad para 250 personas y los ingresos totales de entradas para el evento es de $ 4,846.00, el número de adultos y niños están presentes?

Para resolver el problema con el método de sustitución, siga estos pasos:

1. Expresar el problema de la palabra como un sistema de ecuaciones.

   Puede utilizar la información dada en el problema de la palabra a la creación de dos ecuaciones diferentes. Usted desea resolver cuántas entradas de adulto (la) Y las entradas infantiles (c) vendiste. Si el auditorio tiene capacidad para 250 personas y estaba lleno, la suma de las entradas de adulto y entradas niño debe ser 250.

   Los precios de las entradas también le llevan a los ingresos (o giro) del evento. Los tiempos de precios de entrada de adulto el número de adultos presentes le permite saber la cantidad de dinero que usted hizo de los adultos. Usted puede hacer el mismo cálculo con los boletos de niño. La suma de estos dos cálculos debe ser el ingreso total de entradas para el evento.

   He aquí cómo usted escribe este sistema de ecuaciones:

   

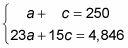
2. Resolver para una de las variables.

   Escoja la variable con un coeficiente de 1 si se puede, porque la solución para esta variable será fácil. Para este ejemplo, se puede optar por resolver la en la primera ecuación. Para ello, restar c desde ambos lados: la = 250 - c.

   Siempre se puede mover cosas de un lado de una ecuación a la otra, pero no caer en la trampa que 250 - c es 249c, como algunas personas lo hacen. Los que no son términos semejantes, por lo que no puede combinarlos.

3. Sustituya la variable resuelto en la otra ecuación.

   En este ejemplo, a resolver por la en la primera ecuación. Se toma este valor (250 - c) Y sustituirlo en la otra ecuación para la. (Asegúrese de que no sustituyen en la ecuación que utilizó en el paso 1 de lo contrario, se le va en círculos.)

   La segunda ecuación dice ahora 23 (250 - c) + 15c = 4.846.

4. Resolver para la variable desconocida.

   Al distribuir el número 23, se obtiene 5750 - 23c + 15c = 4.846. Al simplificar esto, usted consigue 5750 - 8c = 4,846, o -8c = -904. Por lo tanto, c = 113. Un total de 113 niños asistieron al evento.

5. Sustituir el valor de la variable desconocida en una de las ecuaciones originales para resolver para la otra variable desconocida.

   Usted no tiene que sustituir a una de las ecuaciones originales, pero sus respuestas tienden a ser más preciso si lo hace.

   Al conectar 113 en la primera ecuación de c, usted obtiene la + 113 = 250. Resolviendo esta ecuación, se obtiene la = 137. Usted vendió un total de 137 entradas de adulto.

6. Revise su solución.

   Cuando se conecta la y c en las ecuaciones originales, usted debe conseguir dos afirmaciones verdaderas. Hace 137 + 113 = 250? Sí. Hace 23 (137) + 15 (113) = 4846? Ciertamente.

Con el proceso de eliminación

Si la solución de un sistema de dos ecuaciones con el método de sustitución resulta difícil o el sistema involucra fracciones, el método de eliminación es su mejor opción. (¿Quién quiere tratar con fracciones de todos modos?) En el método de eliminación, a tomar una de las variables cancelar sí mismo mediante la adición de las dos ecuaciones.

A veces, hay que multiplicar una o ambas ecuaciones por constantes con el fin de añadir el ecuaciones- esta situación se produce cuando no se puede eliminar una de las variables con sólo añadir las dos ecuaciones juntos. (Recuerde que para que una variable a ser eliminado, los coeficientes de una variable deben ser opuestos.)

Por ejemplo, los pasos siguientes muestran cómo resolver el sistema

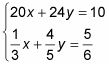
utilizando el proceso de eliminación:

1. Vuelva a escribir las ecuaciones, si es necesario, para que al igual que las variables se alinean debajo de la otra.

   El orden de las variables no materia- sólo asegúrese de que los términos semejantes se alinea con términos como de arriba a abajo. Las ecuaciones en este sistema tienen las variables X y y alineado ya:

   

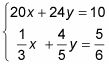
2. Multiplique las ecuaciones por constantes para hacer un conjunto de coeficientes de las variables de los partidos.

   Decida qué variable que desea eliminar.

   Digamos que usted decide eliminar la X variables- primero, usted tiene que encontrar su mínimo común múltiplo. ¿A qué número 20 y 1/3 tanto entrar en? La respuesta es 60. Pero uno de ellos tiene que ser negativo para que cuando se agrega las ecuaciones, los términos se anulan (por eso se llama eliminación!). Multiplique la ecuación superior por -3 y la ecuación final por 180. (Asegúrese de distribuir este número a cada término - incluso en el otro lado del signo igual.) Hacer esto le da lo siguiente:

   

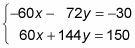
3. Añadir las dos ecuaciones.

   Ahora tiene 72y = 120.

4. Resolver para la variable desconocida que queda.

   Dividiendo por 72 le da

   

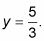
5. Sustituya el valor de la variable se encuentra en cualquiera de las ecuaciones.

   En este ejemplo, se utiliza la primera ecuación:

   

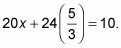
6. Resolver para la variable desconocida final.

   Se termina con

   

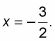
7. Revise sus soluciones.

   Siempre verifique su respuesta al conectar las soluciones de nuevo en el sistema original.

   

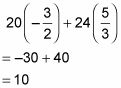
   ¡Funciona! Ahora compruebe la otra ecuación:

   

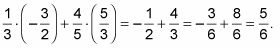
   Debido a que ambos valores son soluciones a ambas ecuaciones, la solución del sistema es correcta.