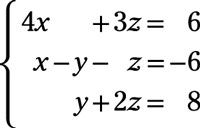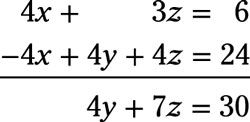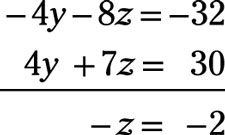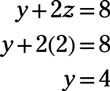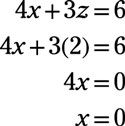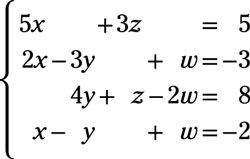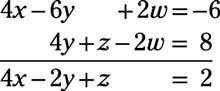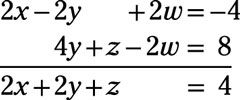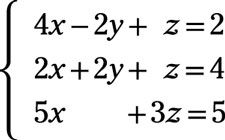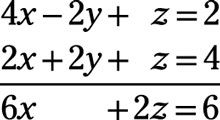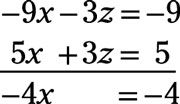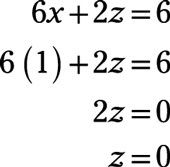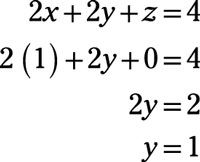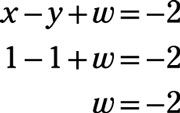Sistemas de ecuaciones utilizadas en pre-cálculo
LA sistema de ecuaciones es una colección de dos o más ecuaciones que implican dos o más variables. Si el número de ecuaciones es igual al número de variables diferentes, entonces usted puede ser capaz de encontrar una solución única que es común a todas las ecuaciones.
Tener el número correcto de las variables no es una garantía que usted tendrá esa solución, y no es terrible si una solución única no existe- a veces sólo escribir una regla para representar las muchas soluciones compartidas por las ecuaciones de la colección .
Usted va a trabajar en los sistemas de ecuaciones en las formas siguientes problemas:
Usando la sustitución para resolver sistemas lineales y no lineales de ecuaciones
Aplicando el método de eliminación cuando los sistemas de ecuaciones lineales
Escribir una regla para múltiples soluciones de sistemas de ecuaciones
Creación de fracciones parciales utilizando descomposición en fracciones
Escribir matrices de coeficientes y matrices constantes para su uso en soluciones de matriz de sistemas
La determinación de matrices inversas a utilizar en los sistemas de ecuaciones lineales
Cuando se trabaja con sistemas de ecuaciones, algunos desafíos incluirán
Reconociendo que la respuesta puede ser sin solución
Distribuir correctamente cuando se utiliza la solución de sustitución para los sistemas
Realización de las operaciones de la matriz correctamente al hacer reducciones de fila y términos eliminando
Escribir soluciones desde resultante matrices variables
Problemas de práctica
Resuelve cada sistema de ecuaciones. Escribe la solución como una terna ordenada, (X, y, z).
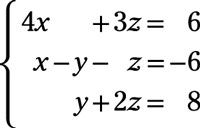
Responder: (0, 4, 2)
Eliminar X en la primera ecuación. Para ello, multiplicar la segunda ecuación (X - y - z = -6) Por -4 y agregarlo a la primera ecuación:
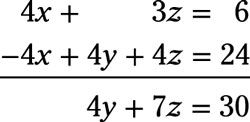
Ahora utilizar esta nueva ecuación y la tercera ecuación original para eliminar y. Multiplique la tercera ecuación (y + 2z = 8) -4 y agregarlo a la nueva ecuación:
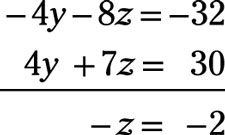
Multiplica cada lado de la ecuación por -1 para obtener z = 2.
Sustituto 2 para z en la tercera ecuación original para resolver y:
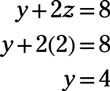
Para resolver X, sustituir 2 para z en la primera ecuación original:
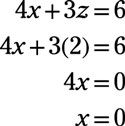
En (X, y, z) La forma, la respuesta es (0, 4, 2).
Resolver el sistema de ecuaciones. Escribe la solución como (X, y, z, w):
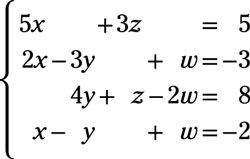
Responder: (1, 1, 0, -2)
Empiece por eliminar la w término. Multiplicar la segunda ecuación (2X - 3y + w = -3) Por 2 y añadirlo a la tercera ecuación:
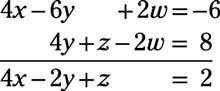
A continuación, multiplique la cuarta ecuación (X - y + w = -2) Por 2 y añadirlo a la tercera ecuación:
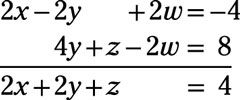
El nuevo sistema de ecuaciones, sin la y plazo, se compone de estas dos nuevas ecuaciones y la primera ecuación original:
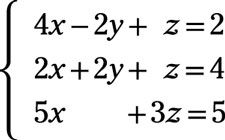
El siguiente paso implica la eliminación de la y término. Añadir las dos primeras ecuaciones del nuevo sistema en conjunto:
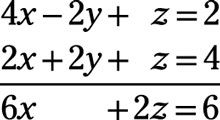
Cada término en la nueva ecuación es divisible por 2, que le da 3X + z = 3. Multiplicar los términos de esta ecuación por -3 y agregarlo a la última ecuación en el nuevo sistema:
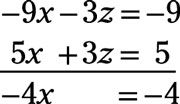
Dividiendo por -4, usted tiene X = 1. Ahora, de vuelta-de resolver para encontrar los valores del resto de las variables:
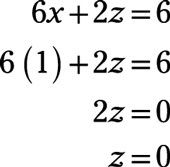
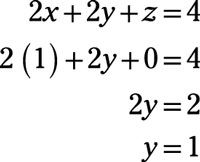
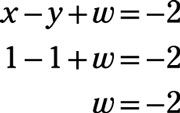
En (X, y, z, w) La forma, la respuesta es (1, 1, 0, -2).
Sobre el autor
 Resolución de ecuaciones de valor absoluto
Resolución de ecuaciones de valor absoluto Una ecuación de valor absoluto lineal es una ecuación que toma la forma |hacha + b| = c. Tomando la ecuación a su valor nominal, usted no sabe si debe cambiar lo que está en entre las barras de valor absoluto a su opuesto, porque no sabes si la…
 Resolver dos ecuaciones lineales algebraicamente
Resolver dos ecuaciones lineales algebraicamente Una solución de un sistema de dos ecuaciones lineales consiste en los valores de X y y que hacen ambas de las ecuaciones verdaderos - al mismo tiempo. Gráficamente, la solución es el punto donde las dos líneas se cruzan. Los dos métodos más…
 Sistemas de ecuaciones lineales en álgebra ii
Sistemas de ecuaciones lineales en álgebra ii En Álgebra II, Ecuación linear consta de términos variables cuyos exponentes son siempre el número 1. Cuando usted tiene dos variables, la ecuación puede ser representado por una línea. Con tres términos, se puede dibujar un plano para…
 Los sistemas con tres ecuaciones lineales
Los sistemas con tres ecuaciones lineales Cuando se trabaja con sistemas de ecuaciones, puede resolver por una variable a la vez. Así, si una tercera ecuación lineal viene a lo largo (con lo cual, por supuesto, su variable z), Así, tres son multitud. Sin embargo, se puede tratar…
 Los fundamentos de la resolución de ecuaciones de álgebra i
Los fundamentos de la resolución de ecuaciones de álgebra i Uno de los objetivos más comunes en álgebra I es resolver una ecuación. Resolver una ecuación significa para identificar el número o números que puede reemplazar la variable con hacer una declaración verdadera. Usted encontrará el factoring…
 Sistemas de ecuaciones de álgebra Resolver
Sistemas de ecuaciones de álgebra Resolver En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una…
 ¿Cómo resolver sistemas lineales que tienen más de dos ecuaciones
¿Cómo resolver sistemas lineales que tienen más de dos ecuaciones Cuando su instructor de pre-cálculo le pide que resolver grandes sistemas de ecuaciones lineales, estas ecuaciones involucrarán más de dos ecuaciones que van junto con más de dos variables. Usted puede escribir estos sistemas más grandes de la…
 ¿Cómo resolver sistemas lineales mediante la sustitución o eliminación
¿Cómo resolver sistemas lineales mediante la sustitución o eliminación Cuando la solución de sistemas lineales, tiene dos métodos - sustitución o eliminación - a su disposición, y que uno elige depende del problema. Si el coeficiente de cualquier variable es 1, lo que significa que usted puede solucionar…
 ¿Cómo resolver sistemas que tienen más de dos ecuaciones
¿Cómo resolver sistemas que tienen más de dos ecuaciones Los sistemas más grandes de ecuaciones lineales implican más de dos ecuaciones que van junto con más de dos variables. Estos sistemas más grandes se pueden escribir en la forma Ax + By + Cz +. . . = K, donde todos los coeficientes (y K) son…
 Cómo escribir un sistema en forma de matriz
Cómo escribir un sistema en forma de matriz En un sistema de ecuaciones lineales, donde cada ecuación está en la forma Hacha + Por + Cz + . . . = K, puede representar los coeficientes de este sistema en la matriz, llamada matriz de coeficientes. Si todas las variables se alinean entre sí…
 Definición de ecuaciones diferenciales homogéneas y no homogéneas
Definición de ecuaciones diferenciales homogéneas y no homogéneas Con el fin de identificar a una ecuación diferencial no homogénea, primero tiene que sabes lo que es una ecuación diferencial homogénea se parece. También a menudo hay que resolver uno antes de poder resolver el otro.Ecuaciones diferenciales…
 Praxis preparación central: sistemas de ecuaciones
Praxis preparación central: sistemas de ecuaciones El examen de álgebra Praxis Core esperará que usted esté familiarizado con los sistemas de ecuaciones. Ecuaciones con dos variables pueden ser resueltos si van acompañados por una segunda ecuación con al menos una de las variables.Cuando se…