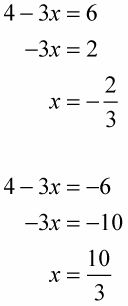Resolución de ecuaciones de valor absoluto
Una ecuación de valor absoluto lineal es una ecuación que toma la forma |hacha + b| = c. Tomando la ecuación a su valor nominal, usted no sabe si debe cambiar lo que está en entre las barras de valor absoluto a su opuesto, porque no sabes si la expresión es positiva o negativa. El signo de la expresión dentro de los bares absolutos de valor todos depende del signo de la variable X. Para resolver una ecuación de valor absoluto en esta forma lineal, usted tiene que considerar dos posibilidades: hacha + b puede ser positivo, o puede ser negativo.
Para resolver para la variable X en |hacha + b| = c, a resolver ambos hacha + b = c y hacha + b = -c.
Por ejemplo, para resolver la ecuación de valor absoluto | 4X + 5 | = 13, se escribe las dos ecuaciones lineales y resolver cada uno para X:
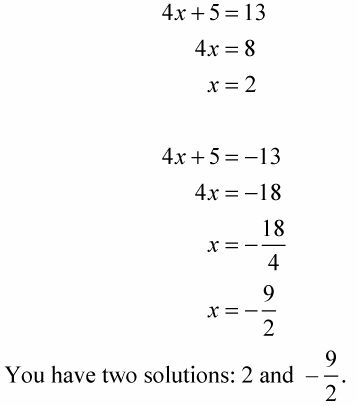
Ambas soluciones funcionan cuando se reemplaza la X en la ecuación original con sus valores.
Una restricción que usted debe tener en cuenta al aplicar la regla para cambiar de valor absoluto a las ecuaciones lineales individuales es que el término valor absoluto tiene que estar solo en un lado de la ecuación.
Por ejemplo, para resolver 3 | 4 - 3X| + 7 = 25, hay que restar 7 de cada lado de la ecuación y luego dividir cada lado por 3:
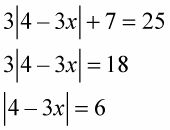
Ahora usted puede escribir las dos ecuaciones lineales y resolverlos para X:
-
1,001 Álgebra practico problemas para los maniquíes -
¿Cómo resolver ecuaciones lineales con división -
¿Cómo resolver ecuaciones lineales con dos multiplicación y división -
¿Cómo resolver ecuaciones lineales con la multiplicación - Vuelva a escribir ecuaciones de valor absoluto como ecuaciones lineales
-
Resolver dos ecuaciones lineales algebraicamente
Los fundamentos de la resolución de ecuaciones de álgebra i Uno de los objetivos más comunes en álgebra I es resolver una ecuación. Resolver una ecuación significa para identificar el número o números que puede reemplazar la variable con hacer una declaración verdadera. Usted encontrará el factoring…
Básico de matemáticas y libro de pre-álgebra para dummies Las reglas para decidir el fin de evaluar expresiones aritméticas, por muy compleja, se llaman el orden de operaciones. El orden completo de las operaciones en matemáticas es:Contenido de paréntesis (y otros símbolos de agrupación) de adentro…
Encontrar el valor absoluto de un número los valor absoluto de un número es el valor positivo de ese número. Le dice a qué distancia de un número es 0 en la recta numérica. El símbolo de valor absoluto es un conjunto de barras verticales.Tomando el valor absoluto de un número…
La negación y el valor absoluto Al adjuntar un signo menos a cualquier número, negar ese número. Negar un número significa cambiar su signo con el signo opuesto, por loColocación de un signo menos para un número positivo hace que sea negativo.Colocación de un signo menos…
Sistemas de ecuaciones de álgebra Resolver En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
¿Cómo resolver desigualdades que contienen valores absolutos Una ecuación de valor absoluto por lo general tiene dos soluciones posibles. Valor absoluto es un poco más complicado de manejar cuando se está resolviendo desigualdades. Las dos soluciones posibles son:Uno donde la cantidad dentro de las barras…
¿Cómo resolver ecuaciones logarítmicas Ecuaciones logarítmicas toman diferentes formas. Como resultado de ello, antes de resolver ecuaciones que contienen los registros, es necesario estar familiarizado con los siguientes cuatro tipos de ecuaciones de registro:Tipo 1. En este tipo, la…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
Resolución de ecuaciones diferenciales separables Ecuaciones diferenciales vuelven más difíciles de resolver el más enredado se vuelven. En ciertos casos, sin embargo, una ecuación que se ve enredado en realidad es fácil de separar. Las ecuaciones de este tipo se llaman ecuaciones separables…
Resolver ecuaciones de trigonometría de factoring El mismo tipo de factoring que el álgebra utiliza para resolver ecuaciones es una gran ayuda en la solución de las ecuaciones de trigonometría. El único truco con las ecuaciones trigonométricas es reconocer que en vez de X's, y's, u otras…
Praxis preparación central: sistemas de ecuaciones El examen de álgebra Praxis Core esperará que usted esté familiarizado con los sistemas de ecuaciones. Ecuaciones con dos variables pueden ser resueltos si van acompañados por una segunda ecuación con al menos una de las variables.Cuando se…