Sistemas de ecuaciones de álgebra Resolver

En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una variable se retira. Por ejemplo:

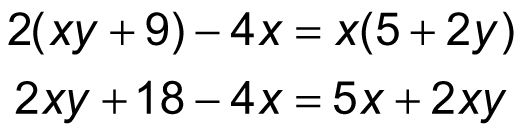
En este punto, puede restar 2xy desde ambos lados de la ecuación:

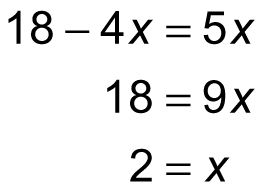
En la mayoría de casos, sin embargo, una ecuación con dos o más variables tiene múltiples soluciones. Para solucionarlo para valores específicos de dos variables, necesita una ecuación adicional - es decir, un sistema de dos ecuaciones.

Sustituyendo para resolver un sistema de ecuaciones

Cuando un sistema de ecuaciones es simple, la forma más fácil de resolver es por sustitución. Por ejemplo:

X + 3 = y3X + y = 7

La primera ecuación que dice que el valor de y en términos de X es X + 3. Para resolver este sistema, sustituto X + 3 para y en la segunda ecuación:

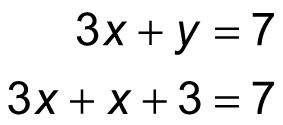
Ahora, esta ecuación tiene una sola variable, por lo que puede resolverlo:

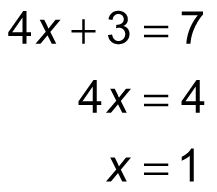
Para encontrar el valor de y, sustituir 1 de X de nuevo en cualquiera de las ecuaciones originales - escoger el más fácil de los dos:

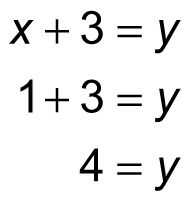
Por lo tanto, en este sistema de ecuaciones, X = 1 y y = 4. He aquí otro ejemplo usando tres variables:

X + y = zX = 2 + y3y = 2z

En este sistema, la segunda ecuación nos dice que X es igual a 2 + y, así que sustituir 2 + y para X en la primera ecuación y simplificar:

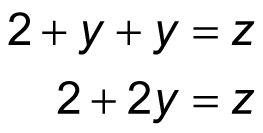
Ahora, usted sabe que z es igual a 2 + 2y, así que esta sustitución para z en la tercera ecuación, entonces resolver y:

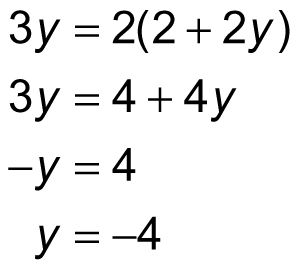
Por lo tanto, y = -4. Sustituya este valor de nuevo en la segunda ecuación:

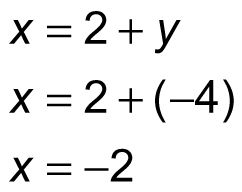
Por lo tanto, X = -2. También puede sustituir -4 para y en la tercera ecuación para encontrar el valor de z:

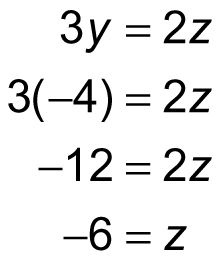
Por lo tanto, en este sistema de ecuaciones, X = -2, y = -4, Y z = -6.

Combinando las ecuaciones para resolver un sistema de ecuaciones

Sustitución funciona bien para resolver sistemas de ecuaciones cuando las ecuaciones están en el lado simple. Pero cuando ecuaciones se ponen más complicadas, una mejor manera de sistema de resolver es mediante la combinación de ecuaciones. Por ejemplo:

12X - 9y = 378X + 9y = 23

Ni ecuación en este sistema hace que borrar el valor de una variable en función de otra, por lo que la sustitución difícil. Para resolver este sistema con más facilidad, añadir las dos ecuaciones como sigue:

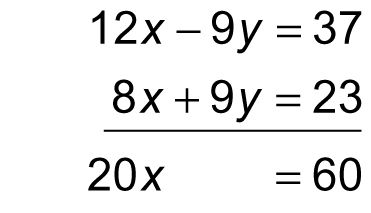
La ecuación resultante, 20X = 60 es muy simple de resolver:

X = 3

Ahora, sustituir este valor por X en cualquiera de las ecuaciones, lo que parece más simple:

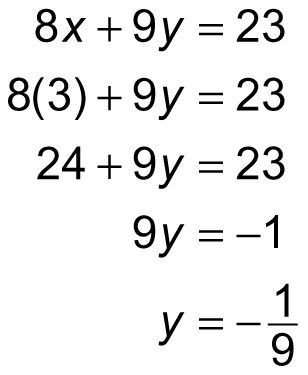
Por lo tanto, en este sistema de ecuaciones, X = 3 y

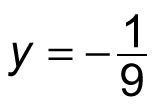
En algunos casos, cuando se utiliza este método para resolver un sistema de ecuaciones, puede que tenga que multiplicar una o ambas ecuaciones por una constante con el fin de hacer que una gota variable de fuera del sistema, como en el ejemplo anterior. Por ejemplo:

2X + 3y = 335X + 4y = 58

En este caso, la adición o sustracción de las dos ecuaciones no harán una variable abandonan. Por lo tanto, desea orientar una variable que desea ver el abandono de las dos ecuaciones cuando están bien sumar o restar. Hacer el X variable de abandono, primero multiplicar la primera ecuación por 5, que es el X coeficiente en la segunda ecuación:

10X + 15y = 1655X + 4y = 58

A continuación, multiplicar la segunda ecuación por 2, que es el X coeficiente en la primera ecuación:

10X + 15y = 16510X + 8y = 116

Observe ahora que las dos ecuaciones comparten el plazo de 10X. Así, puede restar la primera ecuación menos el segundo de la siguiente manera:

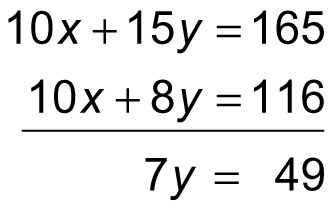
La ecuación resultante, 7y = 49, resuelve fácilmente como sigue:

y = 7

Para resolver X, sustituir 7 para y en cualquiera de las ecuaciones originales parece más fácil trabajar con:

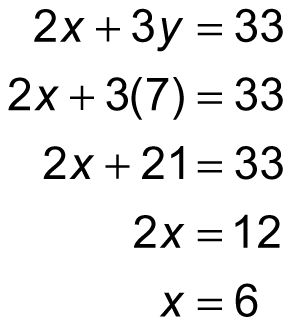
Por lo tanto, en este sistema de ecuaciones, X = 6 y y = 7.