Los sistemas con tres ecuaciones lineales

Cuando se trabaja con sistemas de ecuaciones, puede resolver por una variable a la vez. Así, si una tercera ecuación lineal viene a lo largo (con lo cual, por supuesto, su variable z

), Así, tres son multitud. Sin embargo, se puede tratar fácilmente con todas las variables, siempre y cuando a abordar cada uno de ellos.

A resolver sistemas de tres (o más) ecuaciones lineales usando el método de eliminación:

1. A partir de tres ecuaciones, eliminar una variable para crear dos ecuaciones con dos variables restantes.

   Par la primera ecuación con el segundo, el segundo con el tercero, o el primero con el tercero para eliminar una de las variables. A continuación, elija una pareja diferente y eliminar la misma variable.

2. A partir de esas dos nuevas ecuaciones, eliminar una segunda variable para que pueda resolver por la que permanece.

3. Sustituya nuevo en las otras ecuaciones para encontrar los valores de las otras variables.

   Conecte la primera variable resolviste para en una de las ecuaciones de dos variables que encontró en el paso 1. Luego resolver para la tercera variable enchufando los valores conocidos en una de las ecuaciones originales.

Ejemplo de pregunta

1. Encuentre la solución común del sistema de ecuaciones X + 5y - 2z = 2, 4X + 3y + 2z = 2, y 3X - 3y - 5z = 38.

   X= 4, y = -2, z = -4 - También escrito como la terna ordenada (4, -2, -4). Usted puede optar por eliminar cualquiera de las tres variables, pero por lo general hay una buena-mejor-mejor-peor-peor decisión que se puede hacer.

   En este problema, la mejor opción es eliminar el X variable. los X variable tiene el único coeficiente de 1 en todas las ecuaciones. Usted busca un 1 o -1 o múltiplos del mismo número en los coeficientes de una sola variable.

   Haz dos emparejamientos de la eliminación. Multiplica la primera ecuación por -4 y agregarlo a la segunda ecuación:

   

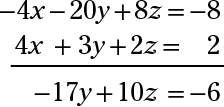
   Para el segundo emparejamiento, multiplicar la primera ecuación por -3 y agregarlo a la tercera ecuación:

   

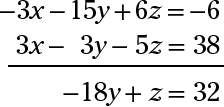
   A continuación, agregue las dos ecuaciones que resultan (después de multiplicar la segunda ecuación por -10 para que pueda eliminar la z's):

   

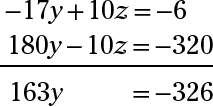
   Divide cada lado de la ecuación por 163 para obtener y = -2. Reemplace la y en -18y + z = 32 con el -2, y se obtiene -18 (-2) + z = 32 36 + z = 32 z = -4.

   Ahora toma los valores de y y z y ponerlas en cualquiera de las ecuaciones originales para resolver X. Usted obtiene X + 5 (-2) - 2 (-4) = 2- X - 10 + 8 = 2- X - 2 = 2- X = 4.

Preguntas de práctica

1. Encuentre la solución común del sistema de ecuaciones 3X + 4y - z = 7, 2X - 3y + 3z = 5, y X + 5y - 2z = 0.

2. Encuentre la solución común del sistema de ecuaciones 8X + 3y - 2z = -2, X - 3y + 4z = -13, Y 6X + 4y - z = -3.

A continuación se presentan las respuestas a las preguntas de la práctica:

1. La respuesta es X = 4, y = -2, z = -3.

   Eliminar X's multiplicando la tercera ecuación por -3 y de añadir a la primera equation- usted consigue -11y + 5z = 7. A continuación, eliminar X's en otra combinación multiplicando la tercera ecuación original por -2 y agregarlo a la segunda equation- usted consigue -13y + 7z Regla = 5. Uso de Cramer en estas dos ecuaciones resultantes:

   

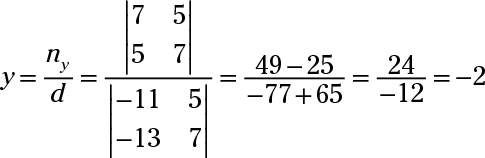
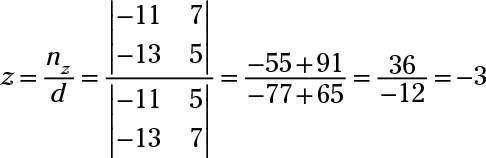
   Ahora sustituir -2 para y y para -3 z en la tercera ecuación original para resolver X. Usted obtiene X + 5 (-2) - 2 (-3) = 0- X - 10 + 6 = 0- X - 4 = 0- X = 4.

2. La respuesta es X = -1, y = 0, z = -3.

   Eliminar z's de multiplicar la primera ecuación por 2 y añadirla a la segunda ecuación para obtener 17X + 3y = -17. Luego de eliminar z's en otra combinación multiplicando la tercera ecuación por 4 y agregarlo a la segunda equation- usted consigue 25X + 13y = -25. Use la regla de Cramer en estas dos ecuaciones resultantes:

   

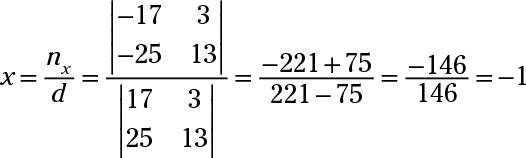
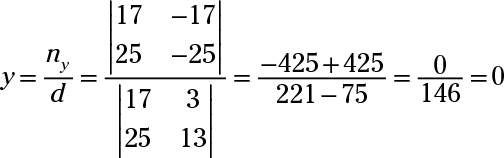
   Ahora sustituir X = -1 Y y = 0 en la tercera ecuación original para obtener 6 (-1) + 4 (0) - z = -3- -6 - z = -3- -z = 3 z = -3.