Cómo escribir un sistema en forma de matriz
En un sistema de ecuaciones lineales, donde cada ecuación está en la forma Hacha + Por + Cz + . . . = K, puede representar los coeficientes de este sistema en la matriz, llamada matriz de coeficientes. Si todas las variables se alinean entre sí verticalmente, entonces la primera columna de la matriz de coeficientes está dedicado a todos los coeficientes de la primera variable, la segunda fila es para la segunda variable, y así sucesivamente. Cada fila representa entonces los coeficientes de cada variable en el orden en que aparecen en el sistema de ecuaciones. A través de un par de diferentes procesos, se puede manipular la matriz de coeficientes con el fin de hacer que las soluciones más fáciles de encontrar.
Resolver un sistema de ecuaciones usando una matriz es un gran método, especialmente para sistemas más grandes (con más variables y más ecuaciones). Sin embargo, estos métodos de trabajo para los sistemas de todos los tamaños, así que tienes que elegir cuál es el método apropiado para que un problema.
Usted puede escribir cualquier sistema de ecuaciones como una matriz. Echa un vistazo a el siguiente sistema:
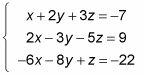
Para expresar este sistema en forma de matriz, usted sigue tres sencillos pasos:
Escribe todos los coeficientes en una sola matriz de primera.
Esto se llama una matriz de coeficientes.
Multiplique esta matriz con las variables del sistema establecido en otra matriz.
Esto a veces se llama el matriz variable.
Introduzca las respuestas en el otro lado del signo igual en otra matriz.
Esto a veces se llama el matriz de respuesta.
La configuración aparece como sigue:
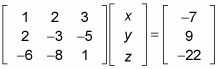
Observe que los coeficientes de la matriz van en orden - se ve una columna para x, y, y z.
Resolver un sistema de ecuaciones en la TI-83 Plus Puede utilizar la TI-83 Plus calculadora gráfica para resolver un sistema de ecuaciones. Tres matrices están asociados con un sistema de ecuaciones lineales: la matriz de coeficientes, la matriz solución, y la matriz aumentada.Por ejemplo, LA, B,…
¿Cómo resolver un sistema de ecuaciones en la TI-84 Plus Las matrices son la herramienta perfecta para sistemas de ecuaciones (cuanto más grandes mejor) resolver. Afortunadamente, se puede trabajar con matrices en la TI-84 Plus. Todo lo que necesitas hacer es decidir el método que desea utilizar.LA-1*…
Comandos de la calculadora de álgebra lineal Las calculadoras gráficas son herramientas maravillosas para ayudar a resolver el álgebra lineal procesos- que le permiten descargar la batería más que el poder del cerebro. Dado que existe una amplia variedad de calculadoras gráficas por ahí,…
Álgebra lineal para dummies Al realizar transformaciones en las funciones trigonométricas, como las rotaciones, es necesario utilizar los valores numéricos de estas funciones. Éstos son algunos de los ángulos más usados comúnmente.Cómo cumplir los requisitos de…
Cómo multiplicar matrices uno por el otro Multiplicando las matrices es muy útil cuando resolver sistemas de ecuaciones. Esto es porque se puede multiplicar una matriz por su inversa en ambos lados del signo igual para obtener finalmente la matriz variable en un lado y la solución para el…
¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…
¿Cómo resolver sistemas lineales que tienen más de dos ecuaciones Cuando su instructor de pre-cálculo le pide que resolver grandes sistemas de ecuaciones lineales, estas ecuaciones involucrarán más de dos ecuaciones que van junto con más de dos variables. Usted puede escribir estos sistemas más grandes de la…
Cómo utilizar la eliminación de Gauss para resolver sistemas de ecuaciones Eliminación de Gauss es probablemente el mejor método para resolver sistemas de ecuaciones, si usted no tiene un programa de calculadora gráfica o del ordenador para ayudarle.Las metas de eliminación de Gauss son para hacer que el elemento de la…
Sistemas de ecuaciones usando determinantes de problemas: la regla de Cramer Si tu profesor de pre-cálculo le pide que resolver un sistema de ecuaciones, puede él o ella impresionar usando la regla de Cramer en lugar de utilizar una calculadora gráfica.La regla de Cramer dice que si el determinante de una matriz de…
Sistemas de ecuaciones utilizadas en pre-cálculo LA sistema de ecuaciones es una colección de dos o más ecuaciones que implican dos o más variables. Si el número de ecuaciones es igual al número de variables diferentes, entonces usted puede ser capaz de encontrar una solución única que es…
Escribir una matriz en forma escalonada reducida Usted puede encontrar el forma escalonada reducida de una matriz para encontrar las soluciones a un sistema de ecuaciones. Aunque este proceso es complicado, poniendo una matriz en forma escalonada reducida es beneficiosa porque esta forma de una…
Escribir una matriz en forma aumentada Una alternativa a la escritura de un sistema de ecuaciones como el producto de una matriz de coeficientes y la matriz de variables igualando una matriz de respuesta es lo que se conoce como aumentado forma- este es donde la matriz de coeficientes y…