Álgebra lineal para dummies
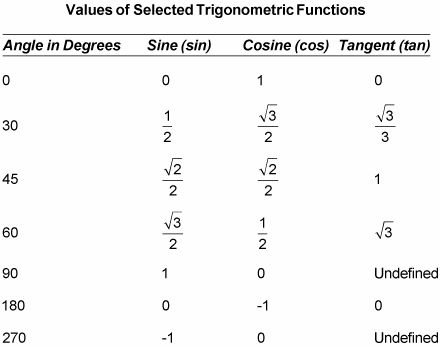
Al realizar transformaciones en las funciones trigonométricas, como las rotaciones, es necesario utilizar los valores numéricos de estas funciones. Éstos son algunos de los ángulos más usados comúnmente.
Cómo cumplir los requisitos de espacio vectorial
En álgebra lineal, que se denomina un conjunto de elementos de un espacio vectorial cuando se cumplen los requisitos particulares. Por ejemplo, deje que un conjunto consiste vectores u, v, y w. También permitirá k y l ser números reales, y considerar las operaciones definidas de oplus- y otimes-. El conjunto es un espacio vectorial si, bajo la operación de oplus-, que cumpla con los siguientes requisitos:
Cierre. u oplus- v está en el conjunto.
Conmutatividad. u oplus- v = v oplus- u.
Asociatividad. u oplus- (v oplus- w) = (u oplus- v) oplus- w.
Un elemento de identidad 0. u oplus- 0 = 0 oplus- u = u para cualquier elemento u.
Un elemento -u inversa. u oplus- -u = -u oplus- u = 0
En virtud de la operación de otimes-, el conjunto es un espacio vectorial si cumple con los siguientes requisitos:
Cierre. k otimes- u está en el conjunto.
Distribución largo de un vector suma. k otimes- (u oplus- v) = k otimes- u oplus- kotimes- v.
La distribución en una suma escalar. (k + l) otimes- u = k otimes-u oplus- l otimes- u.
Asociatividad de un producto escalar. k otimes- (l otimes- u) = (kl) otimes- u.
La multiplicación por la identidad escalar. 1 otimes- u = u.
Algebraica Propiedades que debe saber
Puede utilizar un número de propiedades cuando se trabaja con expresiones algebraicas lineales, incluyendo la conmutativa, asociativa y distributiva de la suma y la multiplicación, así como las identidades y las inversas en la suma y la multiplicación:
Comandos de la calculadora para Álgebra Lineal
Las calculadoras gráficas son herramientas maravillosas para ayudar a resolver el álgebra lineal procesos- que le permiten descargar la batería más que el poder del cerebro. Dado que existe una amplia variedad de calculadoras gráficas por ahí, los siguientes son instrucciones generales para la ayuda con el álgebra lineal que se aplica a la mayoría de las calculadoras gráficas:
Para resolver sistemas de ecuaciones mediante la representación gráfica:
1. Escribe cada ecuación en y = mx + b formulario.
2. ecuaciones Insertar en el y-menú.
3. Gráfico de las líneas.
4. Utilice la herramienta Intersección para obtener la respuesta.
Para agregar o restar matrices:
1. Inserte los elementos en las matrices A y B.
2. Con una nueva pantalla, pulse [A] + [B] o [A] - [B], y pulse Enter.
Para multiplicar por un escalar:
1. Inserte los elementos en la matriz A.
2. Con una nueva pantalla, pulse el escalar y multiplicar: k * [A], y pulse Enter.
Para multiplicar dos matrices juntos:
1. Inserte los elementos en las matrices A y B.
2. Con una nueva pantalla, pulse [A] * [B], y pulse Enter.
Para cambiar filas:
1. Inserte los elementos en una matriz.
2. Uso canje de fila: rowSwap ([nombre de la matriz], primera fila, segunda fila), y pulse Enter.
Para agregar dos filas juntas:
1. Inserte los elementos en una matriz.
2. Uso Además fila: "fila +"([Nombre de la matriz], fila que se añade a apuntar fila, fila de destino) y pulse Enter.
Para agregar el múltiplo de una fila a otra:
1. Inserte los elementos en una matriz.
2. Utilice fila suma-de-múltiple: "*fila +", (Multiplicador, [nombre de la matriz], fila se multiplica, fila de destino que tiene múltiples añadido a la misma), y pulse Enter.
Para multiplicar una fila por un escalar:
1. Inserte los elementos en una matriz.
2. Uso fila múltiple: "* Fila" (multiplicador, [nombre de la matriz], fila) y pulse Enter.
Para crear una forma escalonada:
1. Inserte los elementos en una matriz.
2. Uso fila-escalón forma: árbitro ([nombre de la matriz]) o reducida forma escalonada: rref ([nombre de la matriz]) y pulse Enter.
Para elevar una matriz a una potencia:
1. Inserte los elementos en una matriz.
2. Utilice la operación de intercalación con el poder, p: [Nombre de la matriz] ^ p, y pulse Enter.
Para encontrar inversos:
1. Inserte los elementos en una matriz.
2. Utilice la operación recíproca, X-1: [Nombre de la matriz]-1, y pulse Enter.
Para resolver sistemas de ecuaciones lineales:
(Esto sólo funciona cuando el sistema tiene una única solución- falla cuando la matriz A es singular.)
1. Escribe cada ecuación con las variables en el mismo orden y la constante en el otro lado del signo ecuación.
2. Crear una matriz A, cuyos elementos son los coeficientes de las variables.
3. Crear una matriz B, cuyos elementos son las constantes.
4. Pulse, A-1 * B, y pulse Enter.
El vector resultante tiene los valores de las variables, en orden.
Sobre el autor
Cómo introducir y almacenar matrices en la TI-84 Plus Puede introducir y almacenar matrices en la TI-84 Plus calculadora. LA matriz es una matriz rectangular de números dispuestos en filas y columnas. Las dimensiones, RXC, de una matriz se definen por el número de filas y columnas en la matriz. Los…
¿Cómo resolver un sistema de ecuaciones en la TI-84 Plus Las matrices son la herramienta perfecta para sistemas de ecuaciones (cuanto más grandes mejor) resolver. Afortunadamente, se puede trabajar con matrices en la TI-84 Plus. Todo lo que necesitas hacer es decidir el método que desea utilizar.LA-1*…
Aritmética Matrix en la TI-84 Plus calculadora Puede utilizar la TI-84 Plus calculadora para realizar operaciones aritméticas matriz. Al evaluar expresiones aritméticas que implican matrices, normalmente se quiere realizar las siguientes operaciones básicas: escalar multiplicación, suma,…
Comandos de la calculadora de álgebra lineal Las calculadoras gráficas son herramientas maravillosas para ayudar a resolver el álgebra lineal procesos- que le permiten descargar la batería más que el poder del cerebro. Dado que existe una amplia variedad de calculadoras gráficas por ahí,…
¿Cómo responder a las necesidades de espacio de vectores En álgebra lineal, que se denomina un conjunto de elementos de un espacio vectorial cuando se cumplen los requisitos particulares. Por ejemplo, deje que un conjunto consiste vectores u, v, y w. También permitirá k y l ser números reales, y…
Cómo multiplicar matrices uno por el otro Multiplicando las matrices es muy útil cuando resolver sistemas de ecuaciones. Esto es porque se puede multiplicar una matriz por su inversa en ambos lados del signo igual para obtener finalmente la matriz variable en un lado y la solución para el…
¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…
Cómo escribir un sistema en forma de matriz En un sistema de ecuaciones lineales, donde cada ecuación está en la forma Hacha + Por + Cz + . . . = K, puede representar los coeficientes de este sistema en la matriz, llamada matriz de coeficientes. Si todas las variables se alinean entre sí…
Reglas para sumar y restar matrices Para agregar o restar matrices, hay que operar en sus correspondientes elementos. En otras palabras, se añaden o se quitan la primera fila / primera columna en una matriz hacia o desde el mismo elemento exacta en otra matriz. Las dos matrices deben…
Escribir una matriz en forma escalonada reducida Usted puede encontrar el forma escalonada reducida de una matriz para encontrar las soluciones a un sistema de ecuaciones. Aunque este proceso es complicado, poniendo una matriz en forma escalonada reducida es beneficiosa porque esta forma de una…
Escribir una matriz en forma aumentada Una alternativa a la escritura de un sistema de ecuaciones como el producto de una matriz de coeficientes y la matriz de variables igualando una matriz de respuesta es lo que se conoce como aumentado forma- este es donde la matriz de coeficientes y…
Messing con preguntas de la matriz en la prueba de matemáticas acto De vez en cuando el acto puede deslizarse un problema matriz en la Prueba de Matemáticas. Si usted ve uno, no se asuste. Son fáciles de tratar al revisar el enfoque.Una matriz es simplemente un conjunto de valores. Aunque se pueden realizar varias…
