Escribir una matriz en forma escalonada reducida

Usted puede encontrar el forma escalonada reducida de una matriz para encontrar las soluciones a un sistema de ecuaciones. Aunque este proceso es complicado, poniendo una matriz en forma escalonada reducida es beneficiosa porque esta forma de una matriz es única para cada matriz (y esa matriz única que podría dar las soluciones a su sistema de ecuaciones).

La forma escalonada reducida por filas de una matriz es una matriz con un conjunto muy específico de requisitos. Estos requisitos se refieren a donde las filas de todos 0s se encuentran, así como lo que el primer número en cualquier fila es. Nota: El primer número en una fila de una matriz que no es 0 se denomina coeficiente principal. Para ser considerado para estar en forma escalonada reducida, una matriz debe cumplir todas los siguientes requisitos:

• Todas las filas que contienen todos 0s están en la parte inferior de la matriz.

• Todos los coeficientes principales son 1.

• Cualquier elemento encima o debajo de un coeficiente principal es 0.

• El coeficiente principal de cualquier fila es siempre a la izquierda del coeficiente principal de la fila de debajo de ella.

  
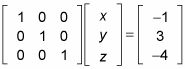  Una matriz (a) en forma escalonada reducida por filas y (b) no en forma escalonada reducida por filas.

Figura una muestra una matriz en forma escalonada reducida, y la figura b no está en forma escalonada reducida debido a que el 7 es directamente sobre el coeficiente principal de la última fila y la 2 está por encima del coeficiente principal en la fila dos.

La forma escalonada reducida por filas de una matriz viene muy bien para sistemas de ecuaciones que son 4 x 4 o más problemas, ya que el método de eliminación supondría una enorme cantidad de trabajo de su parte. El siguiente ejemplo muestra cómo obtener una matriz en forma escalonada reducida utilizando operaciones elementales de fila. Puede utilizar cualquiera de estas operaciones para obtener una matriz en forma escalonada reducida:

• Multiplicar cada elemento en una sola fila por una constante (diferente de cero).

• Intercambiar dos filas.

• Añadir dos filas juntos.

El uso de estas operaciones elementales de fila, puede volver a escribir cualquier matriz de modo que las soluciones al sistema que la matriz representa a ser evidente.

Utilice la forma escalonada reducida solamente si te dicen específicamente que lo haga por un profesor de pre-cálculo o libro de texto. Forma escalonada reducida toma mucho tiempo, energía y precisión. Se puede tomar un montón de pasos, lo que significa que usted puede mezclarse en un montón de sitios. Si usted tiene la opción, usted debe optar por una táctica menos riguroso (a menos que, por supuesto, usted está tratando de mostrar apagado).

Quizás el más famoso (y útil) de la matriz de pre-cálculo es el matriz de identidad, que tiene 1s lo largo de la diagonal desde la esquina superior izquierda a la inferior derecha y tiene 0s en todas partes. Es una matriz cuadrada en forma escalonada reducida y representa el elemento de identidad de la multiplicación en el mundo de las matrices, lo que significa que la multiplicación de una matriz por los resultados de identidad en la misma matriz.

La matriz de identidad es una idea importante en los sistemas de resolver porque si se puede manipular la matriz de coeficientes para parecerse a la matriz identidad (mediante operaciones matriciales legales), entonces la solución al sistema es en el otro lado del signo igual.

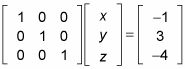
Reescribiendo esta matriz como un sistema produce los valores X = -1, y = 3, y z = -4.

Pero usted no tiene que tomar la matriz de coeficientes hasta aquí sólo para obtener una solución. Usted puede escribir en forma escalonada, como sigue:

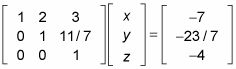
Esta configuración es diferente de la forma escalonada reducida debido a la forma escalonada por filas permite números para estar por encima de los principales coeficientes pero no por debajo.

Reescritura de este sistema le da la siguiente de las filas:

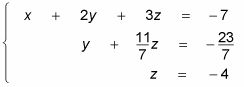
¿Cómo se llega a la solución - los valores de x, y, y z - ¿desde allí? La respuesta a esa pregunta es la resolución de la espalda, también conocido como sustitución hacia atrás. Si una matriz está escrito en forma escalonada por filas, entonces la variable en la fila inferior se ha resuelto por (como z es aquí). Puede conectar este valor en la ecuación anterior para resolver otra variable y continuar este proceso, moviendo su camino hacia arriba (o hacia atrás) hasta que haya resuelto para todas las variables. Al igual que con un sistema de ecuaciones, se pasa de la ecuación más simple a la más compleja.

He aquí cómo se ejecuta la resolución de la espalda: Ahora que usted sabe z = -4, Puede sustituir este valor en la segunda ecuación para obtener y:

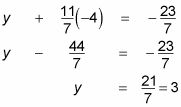
Y ahora que sabes z y y, se puede ir más atrás en la primera ecuación para obtener X:

X + 2 (3) + 3 (-4) = -7

X + 6 - 12 = -7

X - 6 = -7

X = -1