Sistemas de ecuaciones usando determinantes de problemas: la regla de Cramer

Si tu profesor de pre-cálculo le pide que resolver un sistema de ecuaciones, puede él o ella impresionar usando la regla de Cramer en lugar de utilizar una calculadora gráfica.

La regla de Cramer dice que si el determinante de una matriz de coeficientes | A | no es 0, entonces las soluciones a un sistema de ecuaciones lineales se pueden encontrar como sigue:

Si la matriz que describe el sistema de ecuaciones se ve así:

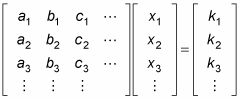
entonces

y así sucesivamente hasta que se haya resuelto para todas las variables. En otras palabras, los componentes de la solución se obtienen fácilmente mediante el cálculo de las proporciones apropiadas de determinantes de una familia de matrices. Observe que el denominador de estos componentes es el determinante de la matriz de coeficientes.

Esta regla es útil cuando los sistemas son muy pequeñas o cuando se puede usar una calculadora gráfica para determinar los factores determinantes porque te ayuda a encontrar soluciones con lugares mínimos para se mezclan. Para utilizarlo, sólo tiene que encontrar el determinante de la matriz de coeficientes.

El determinante de una matriz 2-x-2 como éste:

se define como una d - bc. El determinante de una matriz de 3 x 3 es un poco más complicado. Si la matriz es

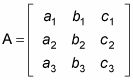
entonces usted puede encontrar el determinante siguiendo estos pasos:

1. Vuelva a escribir las dos primeras columnas inmediatamente después de la tercera columna.

2. Dibuje tres líneas diagonales de la parte superior izquierda a la parte inferior derecha y tres líneas diagonales de la parte inferior izquierda a la esquina superior derecha, como se muestra en esta figura.

   
   ¿Cómo encontrar el determinante de una matriz 3-x-3.

3. Multiplique por las tres diagonales de izquierda a derecha y luego agregar estos productos. Multiplique por los otros tres de izquierda a derecha y añadir estos productos. Luego reste la segunda suma de la primera suma.

   El determinante de la matriz 3-x-3 es:

   

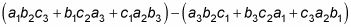
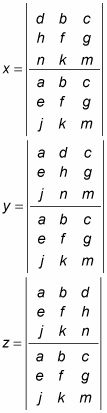
Para encontrar el factor determinante de esta matriz de 3 x 3:

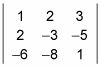
utiliza un proceso conocido como usando diagonales, que se puede ver en esta figura.

Este ejemplo ofrece un acceso directo a encontrar el determinante de una matriz de 3 x 3. Para 4 x 4 y más grandes matrices, los métodos utilizados aquí no son válidas.

Después de encontrar el determinante de la matriz de coeficientes (ya sea a mano o con un dispositivo tecnológico), vuelva a colocar la primera columna de la matriz de coeficientes con la matriz de respuesta desde el otro lado del signo igual y encontrar el determinante de que la nueva matriz. Luego vuelva a colocar la segunda columna de la matriz de coeficientes con la matriz de respuesta y encontrar el determinante de esa matriz. Continúe este proceso hasta que haya reemplazado cada columna y se encontró cada nuevo determinante. Los valores de las respectivas variables son iguales a el determinante de la nueva matriz (cuando se ha sustituido la columna respectiva) dividido por el determinante de la matriz de coeficientes.

No se puede utilizar la regla de Cramer cuando la matriz no es cuadrada o cuando el determinante de la matriz de coeficientes es 0, porque no se puede dividir por 0. regla de Cramer es más útil para la a-2 2-x o superior del sistema de ecuaciones lineales.

Para resolver un sistema de ecuaciones tales como 3-x-3

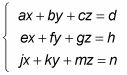
usando la regla de Cramer, configure las variables de la siguiente manera: