Cómo multiplicar matrices uno por el otro

Multiplicando las matrices es muy útil cuando resolver sistemas de ecuaciones. Esto es porque se puede multiplicar una matriz por su inversa en ambos lados del signo igual para obtener finalmente la matriz variable en un lado y la solución para el sistema en el otro.

Por desgracia, la multiplicación de dos matrices juntos no es tan simple como multiplicar los términos correspondientes. Cada elemento de cada matriz se multiplica por cada término de la otra en algún momento.

Para la multiplicación de matrices, las matrices se escriben uno al lado del otro con ningún símbolo en el medio. Si desea multiplicar matrices A y B para conseguir su producto AB, el número de columnas en A debe coincidir con el número de filas de B. Cada elemento de la primera fila de A se multiplica por cada elemento correspondiente de la primera columna de B , y luego todos estos productos se suman para darle el elemento de la primera fila, primera columna de AB. Esto se conoce como teniendo el producto escalar de la primera fila de A con la primera columna de B. Para encontrar el valor en la primera fila, segunda posición de la columna, tomar el producto escalar de la primera fila de A con la segunda columna de B multiplicando cada elemento de la primera fila de A por cada elemento de la segunda columna de B, y luego añadir todos estos productos juntos. Al final, después de todos los posibles productos escalares se calculan, su nueva matriz debe tener el mismo número de filas como A y el mismo número de columnas como B.

Por ejemplo, para multiplicar una matriz A con 3 filas y 2 columnas por una matriz B con 2 filas y 4 columnas, se toma el producto escalar de la primera fila de A con cada una de las columnas de B, produciendo 4 términos en la primera fila del producto AB. Tomando el producto escalar de la segunda fila de A con cada una de las columnas de B produce la segunda fila del producto AB, que contiene otros 4 términos. Y lo mismo vale para la producción de la última fila de AB. Se termina con una matriz de 3 filas y 4 columnas.

Si la matriz A tiene dimensiones m X n y la matriz B tiene dimensiones n X p, AB es una m-X-p matriz. Esta cifra le da una representación visual de la multiplicación de matrices.

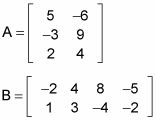
Al multiplicar matrices, no multiplica las partes correspondientes, como cuando se agrega o resta. También, en la multiplicación de matrices, AB no es igual a BA. De hecho, sólo porque usted puede multiplicar A por B no quiere decir puede multiplicar B por A. El número de columnas en A puede ser igual al número de filas en B, pero el número de columnas de B puede no ser igual al número de filas de A. Por ejemplo, se puede multiplicar una matriz con 3 filas y 2 columnas por una matriz con 2 filas y 4 columnas. Sin embargo, no se puede hacer la multiplicación para otro lado porque no se puede multiplicar una matriz con 2 filas y 4 columnas de una matriz con 3 filas y 2 columnas. Si se trató de tomar el producto escalar multiplicando los términos correctos juntos y luego añadir sus productos, en algún punto de la manera que usted se quede sin términos!

He aquí un ejemplo de la multiplicación de matrices. Digamos que un problema le pide que multiplicar las dos matrices siguientes:

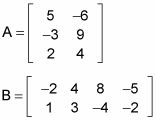
En primer lugar, asegúrese de que usted puede multiplicar las dos matrices. Matriz A es 3 x 2 y B es 2 x 4, por lo que puede multiplicarlos para obtener una matriz de 3-x-4 como una respuesta. Ahora puede proceder a tomar el producto escalar de cada fila de la primera matriz con todas las columnas de la segunda.

Esta cifra establece el proceso para usted. Puede comenzar multiplicando cada término de la primera fila de A por los términos secuenciales en las columnas de la matriz B. Nótese que multiplicar cada entrada en la fila uno a la entrada correspondiente en la columna uno y la adición de estos productos juntos le da la fila uno, columna entrada de uno. Del mismo modo, multiplicar cada entrada en la fila de dos en la entrada correspondiente en la columna tres le da la fila dos, la entrada de la columna de tres.

Teniendo toda la pelusa, la matriz producto es