Cómo aplicar las operaciones básicas de matrices
Al aplicar las operaciones básicas de matrices, funciona muy parecido a operar en múltiples términos dentro parentheses- sólo hay más términos en los "paréntesis" para trabajar. Al igual que con las operaciones sobre los números, un cierto orden está involucrado con la operación en matrices. Multiplicación viene antes de la adición y / o sustracción. Al multiplicar por una escalar, una constante que multiplica una cantidad (que cambia su tamaño o escala), todos y cada elemento de la matriz se multiplica.
Al añadir o restar matrices, que acaba de sumar o restar sus correspondientes términos. Es tan simple como eso. Esta figura muestra cómo sumar y restar dos matrices.
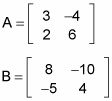
Tenga en cuenta, sin embargo, que se puede sumar o restar matrices solamente si sus dimensiones son exactamente lo mismo. Para agregar o restar matrices, agregar o restar su correspondiente términos- si las dimensiones no son exactamente lo mismo, entonces los términos no se alinearán. Y, obviamente, no se puede sumar o restar términos que no existen!
Al multiplicar una matriz por un escalar, sólo estás multiplicando por una constante. Para ello, se multiplica cada término dentro de la matriz por la constante en el exterior. Utilizando la misma matriz A del ejemplo anterior, usted puede encontrar 3A multiplicando cada término de la matriz A por 3. En este ejemplo se muestra a continuación:
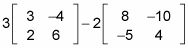
Supongamos que un problema le pide que combina operaciones. Usted simplemente multiplica cada matriz por el escalar por separado y luego sumar o restar ellos. Por ejemplo, considere las dos matrices siguientes:
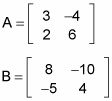
Encuentra 3A - 2B de la siguiente manera:
Inserte las matrices en el problema.
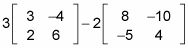
Multiplique los escalares en las matrices.
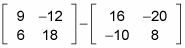
Complete el problema mediante la adición o sustracción de las matrices.
Después de restar, aquí está tu respuesta final:
-
En representación de las matrices en Excel 2007 fórmulas -
Inicializar matrices multidimensionales en C ++ - Java: Uso matrices con dos dimensiones o más
- Cómo hacer aritmética matriz en la r
- Cómo utilizar las operaciones normales en una matriz en la r
-
Editar, la pantalla y aumentar matrices en la TI-83 Plus
Realizar operaciones aritméticas de la matriz en la TI-83 Plus Al evaluar expresiones aritméticas que implican matrices en la calculadora TI-3 Plus gráfica, normalmente se quiere realizar las siguientes operaciones básicas: la multiplicación escalar, negación (inverso aditivo), suma, resta, multiplicación…
Aritmética Matrix en la TI-84 Plus calculadora Puede utilizar la TI-84 Plus calculadora para realizar operaciones aritméticas matriz. Al evaluar expresiones aritméticas que implican matrices, normalmente se quiere realizar las siguientes operaciones básicas: escalar multiplicación, suma,…
Comandos de la calculadora de álgebra lineal Las calculadoras gráficas son herramientas maravillosas para ayudar a resolver el álgebra lineal procesos- que le permiten descargar la batería más que el poder del cerebro. Dado que existe una amplia variedad de calculadoras gráficas por ahí,…
Álgebra lineal para dummies Al realizar transformaciones en las funciones trigonométricas, como las rotaciones, es necesario utilizar los valores numéricos de estas funciones. Éstos son algunos de los ángulos más usados comúnmente.Cómo cumplir los requisitos de…
Cómo multiplicar matrices uno por el otro Multiplicando las matrices es muy útil cuando resolver sistemas de ecuaciones. Esto es porque se puede multiplicar una matriz por su inversa en ambos lados del signo igual para obtener finalmente la matriz variable en un lado y la solución para el…
¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…
Reglas para sumar y restar matrices Para agregar o restar matrices, hay que operar en sus correspondientes elementos. En otras palabras, se añaden o se quitan la primera fila / primera columna en una matriz hacia o desde el mismo elemento exacta en otra matriz. Las dos matrices deben…
Matrices de dimensiones superiores para colecciones de números Arrays bidimensionales pueden ser considerados como la descripción de las tablas de valores, con filas y columnas (como un bloque de celdas en una hoja de cálculo), e incluso las matrices de dimensiones superiores pueden ser considerados como la…
Messing con preguntas de la matriz en la prueba de matemáticas acto De vez en cuando el acto puede deslizarse un problema matriz en la Prueba de Matemáticas. Si usted ve uno, no se asuste. Son fáciles de tratar al revisar el enfoque.Una matriz es simplemente un conjunto de valores. Aunque se pueden realizar varias…
Preparación ASVAB: cómo sumar y restar fracciones Adición y sustracción de fracciones para el ASVAB (o para cualquier otro propósito) puede ser tan simple como multiplicar y dividir, o puede ser más difícil. A medida que la siguiente información muestra, todo depende de si las fracciones…
Militar aptitud de vuelo: operaciones matemáticas para resolver para x La Prueba de Aptitud Vuelo militar podría hacer preguntas que involucran el uso de operaciones matemáticas o expresiones algebraicas. Un expresión algebraica es una colección de números y variables. Usted puede resolver expresiones algebraicas…
Estrategia Ley para multiplicar una matriz vertical mediante una matriz horizontal En el examen ACT de matemáticas, es probable que tenga que multiplicar pares de matrices que tienen ya sea una fila o una columna. Una manera fácil de multiplicar una matriz vertical mediante una matriz horizontal es la creación de una pequeña…