¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz

Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo resolver la ecuación? Se podría dividir ambos lados por 3, lo que es lo mismo que multiplicar por 1.3, para obtener X = 4. Por lo tanto, va con matrices.

En forma de variables, una función inversa se escribe como F ^-1(X), dónde F ^-1 es la inversa de la función f. Usted nombra una matriz inversa de similar la inversa de la matriz A es A^-1. Si A, B y C son matrices en la ecuación matricial AB = C, y se quieren resolver para B, ¿cómo se hace eso? Sólo multiplicar por el inverso de la matriz A (si existe la inversa), que se escribe así:

LA^-1[AB] = A^-1C

Así que la versión simplificada es B = A^-1C.

Ahora que ha simplificado la ecuación básica, es necesario calcular la matriz inversa con el fin de calcular la respuesta al problema.

En primer lugar, debe establecer que sólo las matrices cuadradas tienen inversos - en otras palabras, el número de filas debe ser igual al número de columnas. Y aun así, no todos los matriz cuadrada tiene inversa. Si el determinante de una matriz no es 0, entonces la matriz tiene una inversa.

Cuando una matriz tiene inversa, usted tiene varias maneras de encontrar que, dependiendo de lo grande la matriz es. Si la matriz es una matriz de 2 x 2, entonces usted puede utilizar una fórmula sencilla para encontrar la inversa. Sin embargo, para algo más grande que 2 x 2, debe utilizar un programa de calculadora gráfica o computadora (muchos sitios web pueden encontrar matrices inversas para usted ').

Si usted no utiliza una calculadora gráfica, puede aumentar su matriz original, invertible con la matriz identidad y utilizar las operaciones elementales de fila para obtener la matriz de identidad donde una vez fue su matriz original. Estos cálculos salen de la matriz inversa en la que tuvo la identidad original. Este proceso, sin embargo, es más difícil.

Con eso dicho, aquí es cómo encontrar la inversa de una matriz 2-x-2:

Si la matriz A es la matriz de 2-x-2

su inversa es la siguiente:

Sólo tiene que seguir este formato con cualquier matriz 2-x-2 se le pedirá que encontrar.

Armado con un sistema de ecuaciones y el conocimiento de cómo utilizar matrices inversas, puede seguir una serie de sencillos pasos para llegar a una solución del sistema, utilizando de nuevo la matriz de edad confianza. Por ejemplo, se puede resolver el sistema que sigue utilizando matrices inversas:

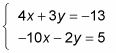
Estos pasos le muestran el camino:

1. Escribe el sistema como una ecuación matricial.

   Cuando se escribe como una ecuación matricial, se obtiene

   

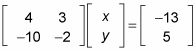
2. Crear la inversa de la matriz de coeficientes de la ecuación matriz.

   Puede utilizar esta fórmula inversa:

   

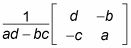
   En este caso, la = 4, b = 3, c = -10, Y d = -2. Por lo tanto ad - bc = 22. Por lo tanto, la matriz inversa es

   

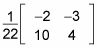
3. Multiplicar la inversa de la matriz de coeficientes en la parte delantera en ambos lados de la ecuación.

   Ahora tiene la siguiente ecuación:

   

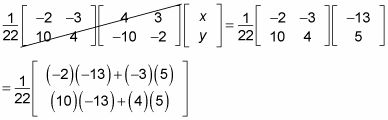
4. Cancelar la matriz de la izquierda y multiplicar las matrices de la derecha.

   Una inversa de la matriz veces una matriz anula. Usted se queda con

   

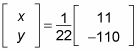
5. Multiplique el escalar para resolver el sistema.

   Terminas con el X y y valores:

   

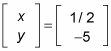
Tenga en cuenta que multiplicar el escalar es generalmente más fácil después de multiplicar las dos matrices.