Resolver un sistema de ecuaciones en la TI-83 Plus
Puede utilizar la TI-83 Plus calculadora gráfica para resolver un sistema de ecuaciones. Tres matrices están asociados con un sistema de ecuaciones lineales: la matriz de coeficientes, la matriz solución, y la matriz aumentada.
Por ejemplo, LA, B, y C, son (respectivamente) la matriz de coeficientes, matriz de solución, y la matriz aumentada para este sistema de ecuaciones:
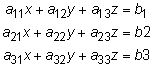
Sistemas de ecuaciones lineales se pueden resolver poniendo primero la matriz aumentada para el sistema de reducción de forma escalonada. La definición matemática de la reducción de forma escalonada no es importante aquí. Es simplemente una forma equivalente del sistema original de ecuaciones, que, cuando se convierte de nuevo en un sistema de ecuaciones, te da las soluciones (si las hay) para el sistema original de ecuaciones.
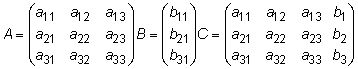
Por ejemplo, cuando la matriz escalonada reducida se convierte en un sistema de ecuaciones, da las soluciones X = -3, y = 3, y z = 9. La matriz se convierte en el sistema de X - z = 0 y y - z = -2. Esta disposición indica que el sistema tiene un número infinito de soluciones - es decir, todas las soluciones en las que X = z y y = z - 2, donde z es cualquier número real.
La tercera foto muestra un sistema que no tiene solución - la última línea de la matriz dice que 0 = 1, que es claramente imposible!
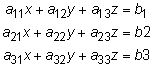
Para resolver un sistema de ecuaciones, siga estos pasos:
Definir la matriz aumentada en el editor Matrix.
Puede definir las matrices de coeficientes y soluciones para el sistema de ecuaciones y luego aumentar estas matrices para formar la matriz aumentada.
Pulse [2nd] [MODO] para acceder a la pantalla de inicio.
prensa
También puede seleccionar la rref comando presionando
pulsando repetidamente
hasta que el cursor se encuentra al lado de la rref comando y pulsando a continuación [ENTER].
Escriba el nombre de la matriz y luego pulse [)].
Para introducir el nombre de la matriz, pulse [Segundo] [X-1] e introduzca el número del nombre de la matriz. (En la TI-83, pulse [MATRX].)
Pulse [ENTER] para poner la matriz aumentada en forma reducida escalonada.
Para encontrar las soluciones (si las hay) para el sistema original de ecuaciones, convertir la matriz escalonada reducida a un sistema de ecuaciones.
-
Copie una matriz a otra en la TI-83 Plus -
Editar, la pantalla y aumentar matrices en la TI-83 Plus -
¿Cómo definir una matriz en la TI-83 Plus -
Realizar operaciones aritméticas de la matriz en la TI-83 Plus -
Evaluar las operaciones determinantes y otra matriz en la TI-84 Plus -
Cómo introducir y almacenar matrices en la TI-84 Plus
¿Cómo resolver un sistema de ecuaciones en la TI-84 Plus Las matrices son la herramienta perfecta para sistemas de ecuaciones (cuanto más grandes mejor) resolver. Afortunadamente, se puede trabajar con matrices en la TI-84 Plus. Todo lo que necesitas hacer es decidir el método que desea utilizar.LA-1*…
Álgebra II: hacer matrices trabajan para usted LA matriz es un arreglo rectangular de números. Cada fila tiene el mismo número de elementos, y cada columna tiene el mismo número de elementos. Las matrices pueden ser clasificados como: cuadrado, identidad, cero, la columna, y así…
Comandos de la calculadora de álgebra lineal Las calculadoras gráficas son herramientas maravillosas para ayudar a resolver el álgebra lineal procesos- que le permiten descargar la batería más que el poder del cerebro. Dado que existe una amplia variedad de calculadoras gráficas por ahí,…
Álgebra lineal para dummies Al realizar transformaciones en las funciones trigonométricas, como las rotaciones, es necesario utilizar los valores numéricos de estas funciones. Éstos son algunos de los ángulos más usados comúnmente.Cómo cumplir los requisitos de…
¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…
¿Cómo resolver sistemas lineales que tienen más de dos ecuaciones Cuando su instructor de pre-cálculo le pide que resolver grandes sistemas de ecuaciones lineales, estas ecuaciones involucrarán más de dos ecuaciones que van junto con más de dos variables. Usted puede escribir estos sistemas más grandes de la…
¿Cómo resolver sistemas que tienen más de dos ecuaciones Los sistemas más grandes de ecuaciones lineales implican más de dos ecuaciones que van junto con más de dos variables. Estos sistemas más grandes se pueden escribir en la forma Ax + By + Cz +. . . = K, donde todos los coeficientes (y K) son…
Cómo utilizar la eliminación de Gauss para resolver sistemas de ecuaciones Eliminación de Gauss es probablemente el mejor método para resolver sistemas de ecuaciones, si usted no tiene un programa de calculadora gráfica o del ordenador para ayudarle.Las metas de eliminación de Gauss son para hacer que el elemento de la…
Cómo escribir un sistema en forma de matriz En un sistema de ecuaciones lineales, donde cada ecuación está en la forma Hacha + Por + Cz + . . . = K, puede representar los coeficientes de este sistema en la matriz, llamada matriz de coeficientes. Si todas las variables se alinean entre sí…
Sistemas de ecuaciones usando determinantes de problemas: la regla de Cramer Si tu profesor de pre-cálculo le pide que resolver un sistema de ecuaciones, puede él o ella impresionar usando la regla de Cramer en lugar de utilizar una calculadora gráfica.La regla de Cramer dice que si el determinante de una matriz de…
Sistemas de ecuaciones utilizadas en pre-cálculo LA sistema de ecuaciones es una colección de dos o más ecuaciones que implican dos o más variables. Si el número de ecuaciones es igual al número de variables diferentes, entonces usted puede ser capaz de encontrar una solución única que es…
Escribir una matriz en forma escalonada reducida Usted puede encontrar el forma escalonada reducida de una matriz para encontrar las soluciones a un sistema de ecuaciones. Aunque este proceso es complicado, poniendo una matriz en forma escalonada reducida es beneficiosa porque esta forma de una…