¿Cómo resolver sistemas que tienen más de dos ecuaciones

Los sistemas más grandes de ecuaciones lineales implican más de dos ecuaciones que van junto con más de dos variables. Estos sistemas más grandes se pueden escribir en la forma Ax + By + Cz +. . . = K, donde todos los coeficientes (y K) son constantes. Estos sistemas lineales pueden tener muchas variables, y usted puede resolver esos sistemas, siempre y cuando usted tiene una ecuación única por variable. En otras palabras, mientras que tres variables necesitan tres ecuaciones para hallar una solución única, cuatro variables necesitará cuatro ecuaciones, y diez variables tendría que tener diez ecuaciones, y así sucesivamente. Usted no necesita preocuparse por los sistemas más grandes de ecuaciones no lineales. Eso sería demasiado complicado para la pre-calc, y sistemas lineales más grandes se complica bastante. Para estos tipos de sistemas, las soluciones se pueden encontrar son muy variables:

• Usted puede encontrar ninguna solución.

• Usted puede encontrar una única solución única.

• Usted puede venir a través de un número infinito de soluciones.

El número de soluciones que encuentres depende de cómo las ecuaciones interactúan entre sí. Dado que los sistemas lineales de tres variables describen las ecuaciones de los planos, no líneas (como ecuaciones de dos variables hacen), la solución del sistema depende de cómo los planos se encuentran en el espacio tridimensional con relación a otra. Por desgracia, al igual que en los sistemas de ecuaciones con dos variables, no se puede decir cuántas soluciones tiene el sistema sin hacer el problema. Tratar a cada problema como si tuviera una solución, y si no lo hace, usted ya sea llegar a una declaración de que no es cierto (no hay soluciones) o siempre es cierto (que significa que hay infinitas soluciones).

Normalmente, debe utilizar el método de eliminación más de una vez para resolver sistemas con más de dos variables y dos ecuaciones.

Por ejemplo, supongamos que un problema le pide que resolver el siguiente sistema:

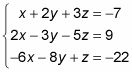
Para encontrar la solución (s), siga estos pasos:

1. Mira los coeficientes de todas las variables y decidir qué variable es más fácil de eliminar.

   Con la eliminación, usted quiere encontrar el mínimo común múltiplo (mcm) de una de las variables, por lo que ir con el que es el más fácil. En este caso, se debe eliminar la X variable.

2. Apartadme dos de las ecuaciones y eliminar una variable.

   En cuanto a las dos primeras ecuaciones, hay que multiplicar la parte superior por -2 y agregarlo a la segunda ecuación. Al hacer esto, se obtiene lo siguiente:

   

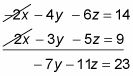
3. Apartadme otras dos ecuaciones y eliminar la misma variable.

   La primera y la tercera ecuaciones permiten eliminar fácilmente X de nuevo. Multiplique la ecuación superior en un 6 y agregarlo a la tercera ecuación para obtener lo siguiente:

   

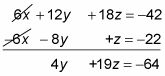
4. Repita el proceso de eliminación con sus dos nuevas ecuaciones.

   Ahora debe tener dos ecuaciones con dos variables:

   

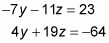
   Tienes que eliminar una de estas variables. En este ejemplo, se elimina la y variable de multiplicando la ecuación 4 por la parte superior y la parte inferior por 7 y luego la adición de las ecuaciones. Esto es lo que le da:

   

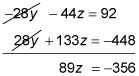
5. Resolver la ecuación final para la variable que queda.

   Si 89z = -356, z = -4.

6. Sustituya el valor de la variable resuelto en una de las ecuaciones que tiene dos variables para resolver por otro.

   En este ejemplo, se utiliza la ecuación de -7y - 11z = 23. Sustituyendo, tienes -7y - 11 (-4) = 23, lo que simplifica a -7y + 44 = 23. Ahora terminar el trabajo:

   

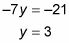
7. Sustituya los dos valores que tiene ahora en una de las ecuaciones originales para resolver la última variable.

   En este ejemplo, se utiliza la primera ecuación del sistema original, que ahora se convierte en X + 2 (3) + 3 (-4) = -7. Simplifique para obtener su respuesta final:

   

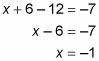
   Las soluciones a esta ecuación son X = -1, y = 3, y z = -4.

Este proceso se llama vuelta de sustitución, ya que, literalmente, para resolver una variable y luego trabajar su camino hacia atrás para resolver los demás. En este ejemplo, se fue de la solución de una variable en una ecuación de dos variables en dos ecuaciones para el último paso con tres variables en tres ecuaciones. . . siempre mueva desde la más simple a la más complicada.