Resolver dos ecuaciones lineales de una sola vez en matemáticas núcleo común

En Common Core matemáticas, estudiantes de octavo grado escribir y resolver sistemas de ecuaciones lineales. Utilizan técnicas simbólicas y soluciones aproximadas de leer gráficos. LA sistema de ecuaciones en el octavo grado es un conjunto de dos ecuaciones, cada uno con las mismas dos variables, y la restricción de que los mismos valores para estas variables deben resolver ambas ecuaciones.

Por ejemplo, supongamos que su tienda de carnicero local vende el 90 por ciento de carne molida sin grasa de $ 3.89 por libra y el 85 por ciento de carne molida sin grasa de $ 3.79 por libra. Si deja que X será el precio de la libra de carne de res magra y puramente y será el precio por libra de grasa de vaca pura, entonces usted puede escribir el siguiente sistema de ecuaciones lineales (el soporte de rizado de la izquierda indica que estas dos ecuaciones van de la mano y que usted está interesado en cualquiera X y y valores que hacen ambas cosas ecuaciones verdaderas al mismo tiempo):

Escribir un sistema de ecuaciones como este requiere hacer un montón de suposiciones sobre el mundo real. Por ejemplo, usted tiene que asumir que no hay tal cosa como la carne de res magra pura y que la carnicería que vendería a usted. Usted también tiene que asumir que la carne molida se hace mezclando carne de res magra puramente junto con grasa de vaca pura y así sucesivamente. Un montón de supuestos - pero incluso si estas suposiciones no son todas válidas, la solución matemática para el sistema todavía le da un punto de partida para hablar de cómo se hacen estas decisiones de precios.

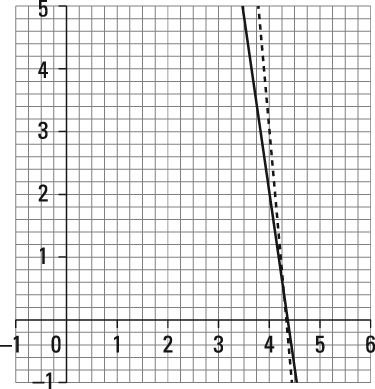
En este caso, se puede leer una solución aproximada de la gráfica en la figura notando donde las dos líneas se cruzan entre sí. Puramente carne magra debe ser un precio de $ 4.29 por libra y grasa de vaca pura en $ 0,29 por libra.

He aquí una breve descripción de una técnica simbólica para resolver este sistema de ecuaciones. Imagínese que usted compró 1,5 libras de 90 por ciento de carne molida sin grasa. A continuación, la primera ecuación en los cambios en el sistema para demostrar que tiene 1,35 libras de carne de res magra, puramente 0.15 libras de grasa de vaca pura, y que usted pagaría $ 5,835. El nuevo sistema de ecuaciones se ve así:

Ambas ecuaciones implican 0.15 libras de grasa de vaca pura, lo que significa que el costo adicional del 90 por ciento de carne molida sin grasa (el 5.835 en la ecuación superior) viene sólo de la carne de vacuno adicional puramente magra. Este adicional de res magra es puramente media libra (la diferencia entre 0,85 y 1,35 libras). Usted puede escribir esta nueva relación como 0.5X = 2.145 (la media libra adicional de carne de res magra puramente cuesta $ 2.145). Puede resolver X Llegar X = 4.29. Esto coincide con el valor que se puede ver en el gráfico. Este tipo de pensamiento se convierte en la técnica algebraica de eliminación. Octavo grado resolver sistemas de ecuaciones lineales por eliminación, así como al trabajar con gráficos.