Estrategias para resolver sistemas de ecuaciones en el acto
LA sistema de ecuaciones
es un conjunto de dos o más ecuaciones que incluyen dos o más variables. Para resolver un sistema de ecuaciones en el examen ACT de matemáticas, necesita una ecuación para cada variable en el sistema. Esto generalmente significa dos ecuaciones y dos variables.Puede resolver un sistema de ecuaciones lineales de dos maneras:
Con la sustitución. Con esta técnica, a resolver una ecuación para una variable en términos de la otra (s), y luego se sustituye este valor en la segunda ecuación.
Mediante la combinación de ecuaciones (eliminación). Para utilizar este método, se añaden o se quitan las dos ecuaciones de tal manera que una variable cae fuera de la ecuación resultante.
Ambos métodos son similares en que le permiten escribir una sola ecuación en una variable, que luego se puede resolver utilizando su bolsa habitual de trucos de álgebra. Después de conocer el valor de una variable, puede sustituir este valor de nuevo en una de las dos ecuaciones originales (generalmente la más fácil) para obtener el valor de la variable restante.
La sustitución es fácil de usar cuando una variable en una ecuación ya está aislado o cuando se puede aislar fácilmente.
Ejemplo 1
Si X + 9 = y y 7X - 2 = 2y, lo que es el valor de xy?
(A) 48
(B) 49
(C) 50
(D) 51
(E) 52
Esta pregunta le da dos ecuaciones con dos variables. En la primera ecuación, y ya está aislado en un lado de la ecuación, por lo que la sustitución debería funcionar bien. Sustituto X + 9 para y en la segunda ecuación:
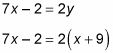
Simplificar y resolver:
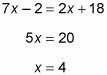
Ahora que ya sabe el valor de X, sustituir este valor en la ecuación que se parece más fácil de trabajar con - en este caso, la primera ecuación - y resolver para y:
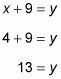
Por lo tanto, X = 4 y y = 13, por lo xy = 52. La respuesta correcta es la opción (E).
La técnica de combinar ecuaciones es fácil de usar cuando ambas ecuaciones contienen esencialmente el mismo plazo. Echa un vistazo a el siguiente ejemplo.
Ejemplo 2
Si 4s + 5t = 9 y 9s + 5t = -11, Lo que es el valor de s + t?
(A) 2
(B) 1
(C) 0
(D) -1
(E) -2
La respuesta a esta pregunta usando la sustitución sería difícil porque ni variable es muy fácil de aislar en un lado de las ecuaciones. Sin embargo, ambas ecuaciones incluyen el término 5t, así que usted puede combinar las dos ecuaciones usando la resta.
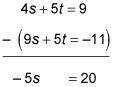
Cuando resta una ecuación de la otra, la t plazo abandona. La ecuación resultante es fácil de resolver:
Como siempre, cuando se conoce el valor de una variable, puede sustituir este valor de nuevo en cualquiera de las ecuaciones - lo que parece más fácil - y resuelve para la otra variable, como este:
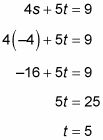
Así s = -4 Y t = 5, significado s + t = 1. Como resultado, la respuesta correcta es Choice (B).
-
Herramientas de álgebra en el menú de la aplicación calculadora TI-Nspire -
Encontrar las intersecciones de las líneas y las parábolas -
¿Cómo resolver ecuaciones lineales con división -
¿Cómo resolver ecuaciones lineales con dos multiplicación y división -
¿Cómo resolver ecuaciones lineales con la multiplicación - Vuelva a escribir ecuaciones de valor absoluto como ecuaciones lineales
Resolución de ecuaciones de valor absoluto Una ecuación de valor absoluto lineal es una ecuación que toma la forma |hacha + b| = c. Tomando la ecuación a su valor nominal, usted no sabe si debe cambiar lo que está en entre las barras de valor absoluto a su opuesto, porque no sabes si la…
Resolver dos ecuaciones lineales algebraicamente Una solución de un sistema de dos ecuaciones lineales consiste en los valores de X y y que hacen ambas de las ecuaciones verdaderos - al mismo tiempo. Gráficamente, la solución es el punto donde las dos líneas se cruzan. Los dos métodos más…
Los sistemas con tres ecuaciones lineales Cuando se trabaja con sistemas de ecuaciones, puede resolver por una variable a la vez. Así, si una tercera ecuación lineal viene a lo largo (con lo cual, por supuesto, su variable z), Así, tres son multitud. Sin embargo, se puede tratar…
Los fundamentos de la resolución de ecuaciones de álgebra i Uno de los objetivos más comunes en álgebra I es resolver una ecuación. Resolver una ecuación significa para identificar el número o números que puede reemplazar la variable con hacer una declaración verdadera. Usted encontrará el factoring…
Sistemas de ecuaciones de álgebra Resolver En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una…
¿Cómo resolver sistemas lineales que tienen más de dos ecuaciones Cuando su instructor de pre-cálculo le pide que resolver grandes sistemas de ecuaciones lineales, estas ecuaciones involucrarán más de dos ecuaciones que van junto con más de dos variables. Usted puede escribir estos sistemas más grandes de la…
¿Cómo resolver sistemas lineales mediante la sustitución o eliminación Cuando la solución de sistemas lineales, tiene dos métodos - sustitución o eliminación - a su disposición, y que uno elige depende del problema. Si el coeficiente de cualquier variable es 1, lo que significa que usted puede solucionar…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
¿Cómo resolver sistemas que tienen más de dos ecuaciones Los sistemas más grandes de ecuaciones lineales implican más de dos ecuaciones que van junto con más de dos variables. Estos sistemas más grandes se pueden escribir en la forma Ax + By + Cz +. . . = K, donde todos los coeficientes (y K) son…
Resolución de ecuaciones diferenciales separables Ecuaciones diferenciales vuelven más difíciles de resolver el más enredado se vuelven. En ciertos casos, sin embargo, una ecuación que se ve enredado en realidad es fácil de separar. Las ecuaciones de este tipo se llaman ecuaciones separables…
Sistemas de ecuaciones utilizadas en pre-cálculo LA sistema de ecuaciones es una colección de dos o más ecuaciones que implican dos o más variables. Si el número de ecuaciones es igual al número de variables diferentes, entonces usted puede ser capaz de encontrar una solución única que es…
Praxis preparación central: sistemas de ecuaciones El examen de álgebra Praxis Core esperará que usted esté familiarizado con los sistemas de ecuaciones. Ecuaciones con dos variables pueden ser resueltos si van acompañados por una segunda ecuación con al menos una de las variables.Cuando se…