Praxis preparación central: sistemas de ecuaciones

El examen de álgebra Praxis Core esperará que usted esté familiarizado con los sistemas de ecuaciones. Ecuaciones con dos variables pueden ser resueltos si van acompañados por una segunda ecuación con al menos una de las variables.

Cuando se presenta este tipo de sistemas de ecuaciones, o sistemas de ecuaciones, el truco es usar la información para obtener una ecuación con una variable. Existen dos métodos principales para lograr esto: el método de sustitución y el método de eliminación.

Resolver por sustitución

los sustitución método implica encontrar el valor de una variable en términos de la otra en una ecuación. A continuación, puede sustituir esa expresión de la variable en la segunda ecuación. El resultado es una ecuación con una variable, y se puede resolver una ecuación con una variable mediante el uso de las técnicas descritas anteriormente.

4X + 2y = 22

X + y = 8

El concepto es que X tiene el mismo valor en ambas ecuaciones y también lo hace y. Para resolver el sistema de ecuaciones usando el método de sustitución, usted indica bien lo y iguales en términos de X o que X iguales en términos de y. Puede utilizar cualquiera de las ecuaciones para hacer la determinación, pero la segunda ecuación es más fácil trabajar con porque ni variable tiene un coeficiente molestos.

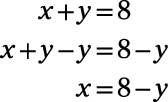
Porque X tiene exactamente el mismo valor que 8 - y, puede sustituir 8 - y para X en la otra ecuación. Entonces usted tiene una ecuación con una sola variable.

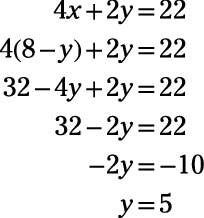
Puede resolver la ecuación para determinar que y = 5. A continuación, puede sustituir 5 para y en cualquiera de las ecuaciones y resolver X, que es 3.

Cuando se utiliza el método de sustitución para resolver un sistema de ecuaciones, asegúrese de que usted no sustituye una expresión variable para la otra variable en la ecuación que utilizó para determinar la expresión. Debe utilizar la otra equation- de lo contrario, el resultado será una ecuación con ninguna variable. Una ecuación con ninguna variable no puede ser resuelto.

Resolver por eliminación

Otro método utilizado para los sistemas de resolución de ecuaciones es de eliminación. Se basa en el hecho de que la adición del mismo valor a o restando el mismo valor de ambos lados de un verdadero resultados de la ecuación en otra ecuación verdadera. En este caso, el valor añadido o restado es lo que está representado por los dos lados de una de las ecuaciones dadas. Echa un vistazo a este ejemplo:

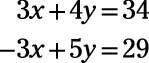
Debido a que ambos lados de la segunda ecuación de (y el primero, para el caso) tienen el mismo valor, la segunda ecuación puede ser añadido a la primera ecuación. El resultado es tercera ecuación que también es cierto.

Eso es una cosa ideal que hacer aquí, porque la adición de 3X y -3X deshacerse X, dejándole una ecuación con una sola variable, y. Los coeficientes de X tener el mismo valor absoluto, por lo que la eliminación puede trabajar inmediatamente. A veces se puede tener que restar.

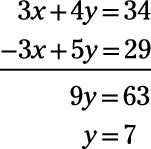
Sabiendo que y = 7, se puede poner en el 7 de y en cualquiera de las ecuaciones para determinar que X = 2.

Con tanto la eliminación y sustitución, poniendo un valor variable en lugar de la variable no causa problemas. Eso sí, no sustituir una expresión algebraica para una variable en la ecuación que le dio la expresión. Ahí es donde el caos espera.

Para utilizar la eliminación cuando ni variable tiene coeficientes con el mismo valor absoluto, se puede multiplicar ambos lados de una ecuación por el mismo número y obtener una nueva ecuación. En algunos casos, usted debe hacer eso a ambas ecuaciones. Considere las siguientes ecuaciones:

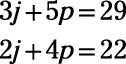
Ni variable tiene coeficientes con el mismo valor absoluto, pero usted puede multiplicar ambos lados de la ecuación arriba por 2 y ambos lados de la ecuación final por 3 para dar j el mismo coeficiente.

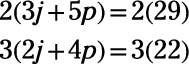
A continuación, puede restar una ecuación de la otra y obtener una ecuación con una variable.

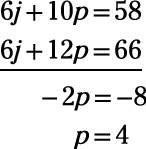
Ahora que usted sabe p = 4, puede sustituir 4 por p en cualquiera de las ecuaciones y resolver j, que tiene un valor de 3.

La sustitución es el método ideal para usar cuando al menos uno de los términos variables tiene un coeficiente de 1 (entiende). La eliminación es el método generalmente preferido para usar cuando ambas variables tienen coeficientes distintos de 1 en todos los casos.