Resolución de problemas de palabras acto utilizando un sistema de ecuaciones
Resolución de problemas de palabras es una de las razones más comunes de utilizar un sistema de ecuaciones. Por ejemplo, algunos problemas de palabras en el examen ACT de matemáticas que sería difícil acercarse utilizando una única variable es relativamente fácil cuando se utiliza más de una variable.
LA sistema de ecuaciones es un conjunto de dos o más ecuaciones que incluyen dos o más variables. Para resolver un sistema de ecuaciones, necesita una ecuación para cada variable en el sistema. Esto generalmente significa dos ecuaciones y dos variables.
Ejemplo
Dorian y Micah han estado ahorrando dinero de sus trabajos de verano. Si Dorian tenía el doble de dinero y Micah tenido la mitad que, junto tendrían $ 2.075. Y si Miqueas tenía el doble de dinero y Dorian tenía la mitad que, en conjunto tendrían $ 2,300. ¿Cuánto dinero tiene Dorian?
(A) $ 800
(B) $ 850
(C) $ 900
(D) $ 950
(E) $ 1.000
Usted podría resolver este problema utilizando una sola variable, pero ese enfoque sería complicado y podría llevar a un error en el camino. En su lugar, utilice dos variables, dejando d el dinero de la igualdad de Dorian y m dinero igual de Miqueas. La creación de dos ecuaciones de la siguiente manera:
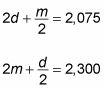
Para eliminar las fracciones, multiplique ambas ecuaciones por 2:
Este sistema de ecuaciones es fácil de resolver mediante la sustitución. Comience por aislamiento m en la primera ecuación:
m = 4150 - 4d
Ahora sustituir 4150 - 4d para m en la segunda ecuación y, a continuación, para resolver d:
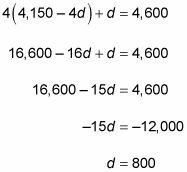
Dorian tiene $ 800, por lo que la respuesta correcta es la opción (A).
-
Herramientas de álgebra en el menú de la aplicación calculadora TI-Nspire -
Encontrar las intersecciones de las líneas y las parábolas -
¿Cómo resolver ecuaciones lineales con la multiplicación -
Resolución de ecuaciones de valor absoluto -
Resolver dos ecuaciones lineales algebraicamente - Sistemas de ecuaciones lineales en álgebra ii
Los sistemas con tres ecuaciones lineales Cuando se trabaja con sistemas de ecuaciones, puede resolver por una variable a la vez. Así, si una tercera ecuación lineal viene a lo largo (con lo cual, por supuesto, su variable z), Así, tres son multitud. Sin embargo, se puede tratar…
Los fundamentos de la resolución de ecuaciones de álgebra i Uno de los objetivos más comunes en álgebra I es resolver una ecuación. Resolver una ecuación significa para identificar el número o números que puede reemplazar la variable con hacer una declaración verdadera. Usted encontrará el factoring…
Sistemas de ecuaciones de álgebra Resolver En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una…
¿Cómo resolver sistemas lineales que tienen más de dos ecuaciones Cuando su instructor de pre-cálculo le pide que resolver grandes sistemas de ecuaciones lineales, estas ecuaciones involucrarán más de dos ecuaciones que van junto con más de dos variables. Usted puede escribir estos sistemas más grandes de la…
¿Cómo resolver sistemas lineales Cuando a resolver sistemas con dos variables y por lo tanto dos ecuaciones, las ecuaciones pueden ser lineales o no lineales. Los sistemas lineales se suelen expresar en la forma Ax + By = C, donde A, B y C son números reales.Cuando la solución de…
¿Cómo resolver sistemas lineales mediante la sustitución o eliminación Cuando la solución de sistemas lineales, tiene dos métodos - sustitución o eliminación - a su disposición, y que uno elige depende del problema. Si el coeficiente de cualquier variable es 1, lo que significa que usted puede solucionar…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
¿Cómo resolver sistemas que tienen más de dos ecuaciones Los sistemas más grandes de ecuaciones lineales implican más de dos ecuaciones que van junto con más de dos variables. Estos sistemas más grandes se pueden escribir en la forma Ax + By + Cz +. . . = K, donde todos los coeficientes (y K) son…
Cómo escribir un sistema en forma de matriz En un sistema de ecuaciones lineales, donde cada ecuación está en la forma Hacha + Por + Cz + . . . = K, puede representar los coeficientes de este sistema en la matriz, llamada matriz de coeficientes. Si todas las variables se alinean entre sí…
Resolución de ecuaciones diferenciales separables Ecuaciones diferenciales vuelven más difíciles de resolver el más enredado se vuelven. En ciertos casos, sin embargo, una ecuación que se ve enredado en realidad es fácil de separar. Las ecuaciones de este tipo se llaman ecuaciones separables…
Sistemas de ecuaciones utilizadas en pre-cálculo LA sistema de ecuaciones es una colección de dos o más ecuaciones que implican dos o más variables. Si el número de ecuaciones es igual al número de variables diferentes, entonces usted puede ser capaz de encontrar una solución única que es…
Praxis preparación central: sistemas de ecuaciones El examen de álgebra Praxis Core esperará que usted esté familiarizado con los sistemas de ecuaciones. Ecuaciones con dos variables pueden ser resueltos si van acompañados por una segunda ecuación con al menos una de las variables.Cuando se…