¿Cómo resolver sistemas no lineales

En un sistema no lineal,

al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación lineal en la forma AX + By = C (donde A, B, y C son números reales) - un sistema no lineal está representada por cualquier otra forma. Ejemplos de ecuaciones no lineales incluyen, pero no se limitan a, cualquier sección cónica, polinomio de grado por lo menos 2, la función racional, exponencial o logarítmica.

¿Cómo resolver un sistema no lineal cuando una ecuación en el sistema es no lineal

Si una ecuación en un sistema no es lineal, puede utilizar la sustitución. En esta situación, puede resolver por una variable en la ecuación lineal y sustituir esta expresión en la ecuación no lineal, porque la solución para una variable en una ecuación lineal es un pedazo de pastel! Y en cualquier momento se puede resolver por una variable fácilmente, puede sustituir esa expresión en la otra ecuación para resolver el otro.

Por ejemplo, siga estos pasos para resolver este sistema:

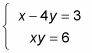
1. Resolver la ecuación lineal de una variable.

   En este ejemplo, la ecuación de arriba es lineal. Si resuelve por X, usted obtiene X = 3 + 4y.

2. Sustituir el valor de la variable en la ecuación no lineal.

   Al conectar 3 + 4y en la segunda ecuación para X, que te dan (3 + 4y)y = 6.

3. Resolver la ecuación no lineal para la variable.

   Al distribuir el y, usted consigue 4y² + 3y = 6. Debido a que esta ecuación es cuadrática, debe obtener 0, por un lado, por lo que resta el 6 de ambos lados para obtener 4y² + 3y - 6 = 0. Hay que usar la fórmula cuadrática para resolver esta ecuación para y:

   

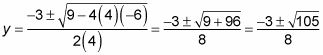
4. Sustituya la solución (s) en cualquiera de las ecuaciones para resolver la otra variable.

   Porque has encontrado dos soluciones para y, usted tiene que sustituir a los dos para conseguir dos pares de coordenadas diferentes. Esto es lo que sucede cuando usted hace:

   

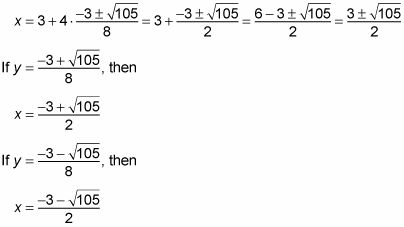
   Por lo tanto, se obtiene las soluciones para el sistema:

   

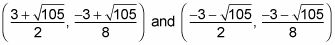
Estas soluciones representan la intersección de la línea X - 4y Y la función racional = 3 xy = 6.

¿Cómo resolver un sistema no lineal cuando ambas ecuaciones del sistema son no lineales

Si las dos ecuaciones en un sistema no lineal son, bueno, sólo tienes que ser más creativos para encontrar las soluciones. A menos que una variable se eleva a la misma potencia en ambas ecuaciones, la eliminación es fuera de la cuestión. Resolviendo para una de las variables en cualquiera de las ecuaciones no es necesariamente fácil, pero por lo general se puede hacer. Después de resolver para una variable, conecte esta expresión en la otra ecuación y resuelve para la otra variable tal como lo hizo antes. A diferencia de los sistemas lineales, muchas operaciones pueden estar involucrados en la simplificación o la resolución de estas ecuaciones. Sólo recuerde para mantener su orden de las operaciones en cuenta en cada paso del camino.

Cuando ambas ecuaciones en un sistema son secciones cónicas, usted nunca encontrará más de cuatro soluciones (a menos que las dos ecuaciones describen la misma sección cónica, en cuyo caso el sistema tiene un número infinito de soluciones - y por lo tanto es un sistema dependiente). Cuatro es el límite porque las secciones cónicas son curvas muy suaves sin esquinas agudas o dobleces locos, así que dos secciones cónicas diferentes no pueden intersectar más de cuatro veces.

Por ejemplo, supongamos que un problema le pide que resolver el siguiente sistema:

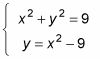
No ese problema simplemente hacer que su piel de gallina? No rompa la loción de calamina por el momento, sin embargo. Siga estos pasos para encontrar las soluciones:

1. Resuelva para x² o Y² en una de las ecuaciones dadas.

   La segunda ecuación es atractiva porque todo lo que tienes que hacer es añadir 9 a ambas partes para llegar y + 9 = X².

2. Sustituya el valor del paso 1 en la otra ecuación.

   Ahora tiene y + 9 + y² = 9 - una ecuación cuadrática.

3. Resolver la ecuación cuadrática.

   Reste 9 de ambas partes para llegar y + y² = 0.

   Recuerde que no está permitido, siempre, para dividir por una variable.

   Usted debe factorizar el máximo común divisor (MCD) en lugar de conseguir y(1 + y) = 0. Utilice la propiedad del producto cero para resolver y = 0 y y = -1.

4. Sustituya el valor (s) de la Etapa 3 en cualquiera de las ecuaciones para resolver la otra variable.

   En este ejemplo se utiliza la ecuación resuelta en el Paso 1. Cuando y es 0, 9 = X², así

   

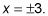
   Cuando y es -1, 8 = X², así

   

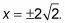
   Asegúrese de mantener un registro de qué solución va con qué variable, ya que hay que expresar estas soluciones como puntos en un par de coordenadas. Sus respuestas son

   

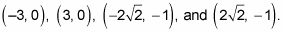
   Este conjunto de soluciones representa las intersecciones del círculo y la parábola dada por las ecuaciones en el sistema.