La identificación, y ecuaciones diferenciales parciales lineales ordinarias
Ecuaciones diferenciales (DES) vienen en muchas variedades. Y diferentes variedades de ED se pueden resolver utilizando diferentes métodos. Puede clasificar DES como Des ordinaria y parcial. Además de esta distinción se pueden distinguir adicionalmente por su orden.
Aquí hay unos ejemplos:
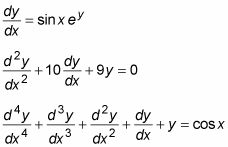
Resolver una ecuación diferencial significa encontrar el valor de la variable dependiente en términos de la variable independiente. Los ejemplos siguientes utilizan y como la variable dependiente, por lo que el objetivo en cada problema es resolver para y en términos de X.
Un ecuación diferencial ordinaria (ODE) tiene sólo derivados de una variable - es decir, no tiene derivadas parciales. Aquí hay algunos ejemplos de EDOs:
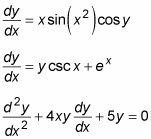
En contraste, una ecuación diferencial parcial (PDE) tiene al menos un derivado parcial. Aquí hay algunos ejemplos de PDE:
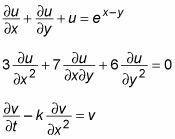
ED se clasifican en función de su orden. Esta clasificación es similar a la clasificación de las ecuaciones polinómicas por grado.
EDO de primer orden sólo contienen primeras derivadas. Por ejemplo:
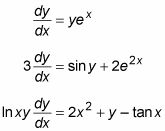
EDO de orden superior se clasifican, como polinomios son, por el mayor orden de sus derivados. Estos son ejemplos de segunda, tercera y cuarta EDO de orden:
Al igual que con polinomios, en general, un orden superior DE es más difícil de resolver que uno de orden inferior.
Lo que constituye una ecuación diferencial lineal depende ligeramente a quién le preguntes. A efectos prácticos, un familiar de primer orden lineal DE encaja en la forma siguiente:
dónde la(X) Y b(X) Son funciones de X. Aquí hay algunos ejemplos de primer orden lineal ED:
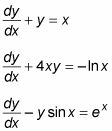
Linear DEs menudo se puede resolver, o al menos simplificada, utilizando una la integración de factor.
Un segundo grado lineal DE encaja en el siguiente formulario:
dónde la, b, y c son todas las constantes. Aquí hay unos ejemplos:
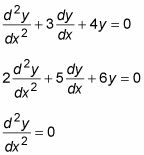
Tenga en cuenta que la constante la siempre se puede reducir a 1, dando lugar a ajustes para los otros dos coeficientes.
-
¿Cómo resolver ecuaciones lineales con dos multiplicación y división -
¿Cómo resolver ecuaciones lineales con la multiplicación -
Resolución de ecuaciones de valor absoluto -
Resolver dos ecuaciones lineales algebraicamente -
Los sistemas con tres ecuaciones lineales -
Los fundamentos de la resolución de ecuaciones de álgebra i
Ecuaciones diferenciales libro para los maniquíes Antes de que pueda resolver una ecuación diferencial, lo que necesita saber de qué tipo es. Hay varios tipos diferentes de ecuaciones, incluyendo lineal, separable, exacta y homogénea, y no homogénea.Ecuaciones diferenciales lineales tratan…
¿Cómo decirle a una ecuación diferencial de otro Antes de que pueda resolver una ecuación diferencial, lo que necesita saber de qué tipo es. Hay varios tipos diferentes de ecuaciones, incluyendo lineal, separable, exacta y homogénea, y no homogénea.Ecuaciones diferenciales lineales tratan…
Analizar un circuito de primer orden rl utilizando métodos LaPlace El uso de la transformada de Laplace como parte de su análisis de circuitos le proporciona una predicción de respuesta del circuito. Analizar los polos de la transformada de Laplace para obtener una idea general del comportamiento de salida. Polos…
Comprobación de soluciones de ecuaciones diferenciales Incluso si usted no sabe cómo encontrar una solución a una ecuación diferencial, siempre se puede comprobar si una propuesta de solución funciona. Esto es simplemente una cuestión de conectar el valor propuesto de la variable dependiente en…
La clasificación de las ecuaciones diferenciales por orden La clasificación más común de ecuaciones diferenciales se basa en el orden. El orden de una ecuación diferencial, simplemente es el fin de su más alta derivada. Usted puede tener las ecuaciones diferenciales de primera, segunda, y de orden…
Ecuaciones diferenciales para los maniquíes La clasificación más común de ecuaciones diferenciales se basa en el orden. El orden de una ecuación diferencial, simplemente es el fin de su más alta derivada. Usted puede tener las ecuaciones diferenciales de primera, segunda, y de orden…
Distinguir entre las ecuaciones diferenciales lineales, separables y exactas Se puede distinguir entre las ecuaciones diferenciales lineales, separables y exactas si usted sabe qué buscar. Tenga en cuenta que puede que tenga que reorganizar una ecuación para identificarlo.Ecuaciones diferenciales lineales involucrar sólo…
¿Cómo resolver sistemas lineales que tienen más de dos ecuaciones Cuando su instructor de pre-cálculo le pide que resolver grandes sistemas de ecuaciones lineales, estas ecuaciones involucrarán más de dos ecuaciones que van junto con más de dos variables. Usted puede escribir estos sistemas más grandes de la…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
Resolución de ecuaciones diferenciales usando un factor de integración Un método inteligente para resolver ecuaciones diferenciales (ED) es en la forma de una ecuación lineal de primer orden. Este método implica multiplicar toda la ecuación por una la integración de factor. Una ecuación lineal de primer orden…
Definición de ecuaciones diferenciales homogéneas y no homogéneas Con el fin de identificar a una ecuación diferencial no homogénea, primero tiene que sabes lo que es una ecuación diferencial homogénea se parece. También a menudo hay que resolver uno antes de poder resolver el otro.Ecuaciones diferenciales…
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden Si usted puede utilizar una ecuación diferencial de segundo orden para describir el circuito que está viendo, entonces usted está tratando con un circuito de segundo orden. Circuitos que incluyen un inductor, condensador y resistencia conectada…