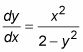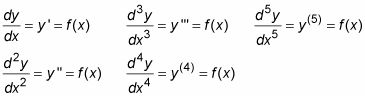La clasificación más común de ecuaciones diferenciales se basa en el orden. El orden de una ecuación diferencial, simplemente es el fin de su más alta derivada. Usted puede tener las ecuaciones diferenciales de primera, segunda, y de orden superior.
primero-ecuaciones diferenciales de orden involucrar a los derivados de primer orden, como en este ejemplo:
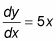
Segundo-ecuaciones diferenciales de orden involucrar a los derivados de segundo orden, como en estos ejemplos:
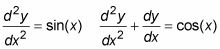
Mayor-ecuaciones diferenciales de orden son aquellos que involucran derivados más altos que el de segundo orden (gran sorpresa en ese nombre inteligente!). Ecuaciones diferenciales de todos los pedidos pueden utilizar el y'Notación, como esto:
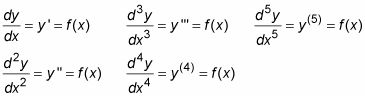
Distinguir entre lineal, separable y Ecuaciones Diferenciales Exactas
Se puede distinguir entre las ecuaciones diferenciales lineales, separables y exactas si usted sabe qué buscar. Tenga en cuenta que puede que tenga que reorganizar una ecuación para identificarlo.
Ecuaciones diferenciales lineales involucrar sólo los derivados de y y los términos de y a la primera potencia, no elevado a cualquier potencia más alta. (Nota: Este es el poder de la derivada es elevado a, no la orden . del derivado) Por ejemplo, esta es una ecuación diferencial lineal porque sólo contiene derivados planteadas a la primera potencia:
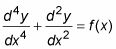
Secuaciones diferenciales eparable se puede escribir de manera que todos los términos en X y todos los términos de y aparecerá en lados opuestos de la ecuación. He aquí un ejemplo:
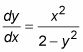
la cual se puede escribir como este con un poco de reorganización:
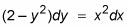
Ecuaciones diferenciales exactas son aquellos en los que se puede encontrar una función cuyo derivadas parciales corresponden a los términos en una ecuación diferencial dada.
Definición de ecuaciones diferenciales homogéneas y no homogéneas
Con el fin de identificar a una ecuación diferencial no homogénea, primero tiene que sabes lo que es una ecuación diferencial homogénea se parece. También a menudo hay que resolver uno antes de poder resolver el otro.
Ecuaciones diferenciales homogéneas involucrar sólo los derivados de y y las condiciones que implica y, y están ajustados a 0, como en esta ecuación:
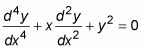
Ecuaciones diferenciales no homogéneas son las mismas que las ecuaciones diferenciales homogéneas, excepto que pueden tener términos que sólo afecten X (y constantes) en el lado derecho, como en esta ecuación:
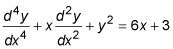
También puedes escribir ecuaciones diferenciales no homogéneas en este formato: y'' + p(X)y'+ q(X)y = g(X). La solución general de esta ecuación diferencial no homogénea es
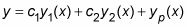
En esta solución, c1y1(X) + c2y2(X) Es la solución general de la correspondiente ecuación diferencial homogénea:
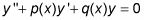
Y yp(X) Es una solución específica para la ecuación no homogénea.
Utilizar el método de coeficientes indeterminados
Si usted necesita encontrar soluciones particulares a las ecuaciones diferenciales no homogéneas, entonces usted puede comenzar con el método de coeficientes indeterminados. Supongamos que se enfrenta la siguiente ecuación diferencial no homogénea:
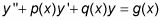
los método de coeficientes indeterminados señala que cuando encuentre una solución candidato, y, y conectarlo a la izquierda, lado de la ecuación, usted termina con g(X). Porque g(X) Es sólo una función de X, a menudo se puede adivinar la forma de yp(X), Hasta coeficientes arbitrarios, y luego resolver esos coeficientes de enchufar yp(X) En la ecuación diferencial.
Este método funciona porque usted está tratando solamente con g(X), Y la forma de g(X) A menudo puede decir lo que una solución particular se parece.
¿Cómo decirle a una ecuación diferencial de otro
Resolución de ecuaciones diferenciales mediante transformada de Laplace soluciones
Los fundamentos de la evaluación de las ecuaciones
Comprobación de soluciones de ecuaciones diferenciales
La clasificación de las ecuaciones diferenciales por orden
Distinguir entre las ecuaciones diferenciales lineales, separables y exactas
La identificación, y ecuaciones diferenciales parciales lineales ordinarias
Resolución de ecuaciones diferenciales separables
Resolución de ecuaciones diferenciales usando un factor de integración
Definición de ecuaciones diferenciales homogéneas y no homogéneas
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden
Encuentra la respuesta de estado cero de un circuito paralelo rl