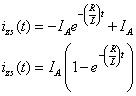Encuentra la respuesta de estado cero de un circuito paralelo rl
Un primer orden circuito en paralelo RL tiene una resistencia (o de la red de resistencias) y un único inductor. Circuitos de primer orden pueden ser analizadas usando las ecuaciones diferenciales de primer orden. Mediante el análisis de un circuito de primer orden, se puede entender el momento y retrasos.
Para encontrar la respuesta total de un circuito paralelo RL como el que se muestra aquí, es necesario encontrar la respuesta a entrada cero y la respuesta de estado cero y luego sumarlos.
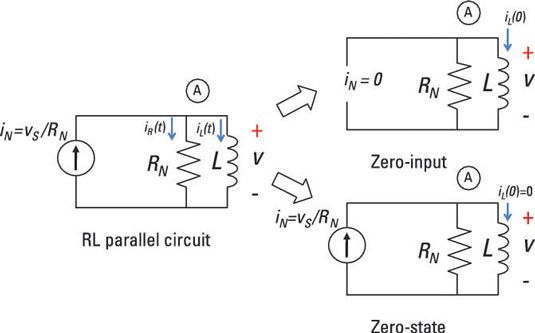
Después de tocar el violín con las matemáticas, se determina que la respuesta de entrada cero del circuito de la muestra es la siguiente:
Ahora ya está listo para calcular la respuesta de estado cero para el circuito. Respuesta Zero-estado significa condiciones iniciales nulas. Para el circuito de estado cero mostrado antes, cero condiciones iniciales significa mirar el circuito con corriente del inductor cero en t lt; 0. Usted necesita encontrar las soluciones homogéneas y particulares para obtener la respuesta de estado cero.
A continuación, usted tiene condiciones iniciales nulas y una corriente de entrada de yoN(t) = u (t), dónde u (t) es una entrada escalón unitario.
Cuando la entrada de paso u (t) = 0, la solución de la ecuación diferencial es la solución yoh(t):
La corriente del inductor yoh(t) es la solución a la ecuación diferencial de primer orden homogénea:
Esta solución es la solución general para la entrada cero. Usted encuentra la constante c1 después de encontrar la solución particular y la aplicación de la condición inicial de no corriente del inductor.
Tiempo después t = 0, una entrada escalón unitario describe la corriente del inductor transitoria. La corriente del inductor para esta entrada escalón se llama respuesta al escalón.
Usted encontrará la solución particular yop(t) estableciendo la entrada escalonada u (t) igual a 1. Para una entrada escalón unitario yoN(t) = u (t), sustituto u (t) = 1 en la ecuación diferencial:
La solución particular yop(t) es la solución para la ecuación diferencial cuando la entrada es un paso unidad u (t) = 1 después de t = 0. Debido u (t) = 1 (una constante) después de la hora t = 0, asumir una solución particular yop(t) es una constante yoLA.
Debido a que la derivada de una constante es 0, lo siguiente es cierto:
Sustituto yop(t) = yoLA en la ecuación diferencial de primer orden:
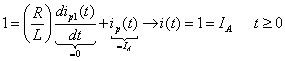
La solución particular finalmente sigue la forma de la entrada porque la entrada cero (o respuesta libre) disminuye a 0 en el tiempo. Usted puede generalizar el resultado cuando el paso de entrada tiene la fuerza yoLA o yoLAu (t).
Es necesario añadir la solución homogénea yoh(t) y la solución particular yop(t) para obtener la respuesta de estado cero:
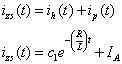
A t = 0, la condición inicial es 0 porque se trata de un cálculo de estado cero. Encontrar c1, aplicar yoZS(0) = 0:
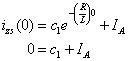
La solución para c1 te dio
C1 = -ILA
Sustituyendo c1 en la respuesta de estado cero yoZS(t), terminas con
-
Encontrar las intersecciones de las líneas y las parábolas -
¿Cómo decirle a una ecuación diferencial de otro -
Analizar un circuito de primer orden rl utilizando métodos LaPlace - Encontrar las raíces de una ecuación factorizada
-
Definición de ecuaciones diferenciales homogéneas y no homogéneas -
Analizar un circuito de primer orden rc usando métodos LaPlace
Analizar un circuito RC serie usando una ecuación diferencial Un circuito en serie RC de primer orden tiene una resistencia (o de la red de resistencias) y un condensador conectado en serie. De primer orden circuitos RC se pueden analizar utilizando ecuaciones diferenciales de primer orden. Mediante el…
Analizar un circuito RLC utilizando métodos LaPlace El uso de la transformada de Laplace como parte de su análisis de circuitos le proporciona una predicción de respuesta del circuito. Analizar los polos de la transformada de Laplace para obtener una idea general del comportamiento de salida. Polos…
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden Si usted puede utilizar una ecuación diferencial de segundo orden para describir el circuito que está viendo, entonces usted está tratando con un circuito de segundo orden. Circuitos que incluyen un inductor, condensador y resistencia conectada…
Componentes de la electrónica: la retroalimentación en los amplificadores de bucle cerrado Si usted está interesado en la comprensión de cómo funciona el circuito de realimentación, recuerde esta regla de amplificadores operacionales electrónicos: Si la tensión de entrada es otra cosa que no sea cero, el amplificador operacional se…
Componentes de la electrónica: cómo utilizar un amplificador operacional como un amplificador de ganancia unitaria LA amplificador de ganancia unitaria es un circuito amplificador electrónico que no amplifica. En otras palabras, tiene una ganancia de 1. La tensión de salida en un amplificador de ganancia unidad es la misma que la tensión de entrada.Usted…
Medidor de máxima transferencia de potencia utilizando ª & # 233-venin de y los teoremas de norton Th # teoremas de Norton de 233-venin y se pueden utilizar para analizar circuitos complejos, centrándose en los circuitos de fuente y carga. Una aplicación de Th # 233-venin de y los teoremas de Norton es calcular la potencia máxima para un…
Cómo detectar un impulso faltante con un circuito de temporización Cuando el tiempo es apagado en su ordenador, eventos específicos no se presentan en el orden correcto. Pero si usted sabe la física y yo-v relaciones de resistencias y condensadores, puede crear un circuito que pulses- detecta a continuación,…
¿Cómo resolver ecuaciones diferenciales usando amplificadores operacionales El circuito amplificador operacional puede resolver ecuaciones matemáticas rápidas, incluyendo problemas de cálculo, tales como las ecuaciones diferenciales. Para resolver una ecuación diferencial mediante la búsqueda v (t), por ejemplo,…
Analizar un circuito RL paralelo usando una ecuación diferencial Un primer orden circuito en paralelo RL tiene una resistencia (o de la red de resistencias) y un único inductor. Circuitos de primer orden pueden ser analizadas usando las ecuaciones diferenciales de primer orden. Mediante el análisis de un…
Analizar un segundo orden circuito paralelo RLC utilizando la dualidad Circuitos RLC de segundo orden tienen una resistencia, inductor, y el condensador conectado en serie o en paralelo. Para analizar un circuito paralelo de segundo orden, se sigue el mismo proceso para el análisis de un circuito serie RLC.Aquí hay…
Encuentra la respuesta total de un circuito paralelo rl Después de encontrar la respuesta a entrada cero y la respuesta de estado cero de un circuito RL en paralelo, usted puede encontrar fácilmente la respuesta total del circuito. Recuerde que un circuito RL paralelo primer orden tiene una resistencia…
Encuentra la respuesta total de un circuito RC serie Después de encontrar la respuesta a entrada cero y la respuesta de estado cero de un circuito en serie RC, usted puede encontrar fácilmente la respuesta total del circuito. Recuerde que un circuito en serie RC de primer orden tiene una resistencia…