Analizar un circuito de primer orden rl utilizando métodos LaPlace
El uso de la transformada de Laplace como parte de su análisis de circuitos le proporciona una predicción de respuesta del circuito. Analizar los polos de la transformada de Laplace para obtener una idea general del comportamiento de salida. Polos reales, por ejemplo, indican el comportamiento de salida exponencial.
Siga estos pasos básicos para analizar un circuito utilizando técnicas de Laplace:
Desarrollar la ecuación diferencial en el dominio del tiempo usando las leyes de Kirchhoff y las ecuaciones de los elementos.
Aplicar la transformación de Laplace de la ecuación diferencial para poner la ecuación en la s-dominio.
Algebraicamente resolver para la solución, o la respuesta transformar.
Aplicar la transformación inversa de Laplace para producir la solución de la ecuación diferencial original descrito en el dominio del tiempo.
Para sentirse cómodo con este proceso, sólo hay que practicar su aplicación a diferentes tipos de circuitos tales como un RC (resistencia-condensador) de circuito, un RL (resistor-inductor) del circuito, y un (resistor-inductor-condensador) circuito RLC .
Aquí es un circuito RL que tiene un interruptor que ha estado en la posición A por un largo tiempo. El interruptor se mueve a la posición B en el tiempo t = 0.
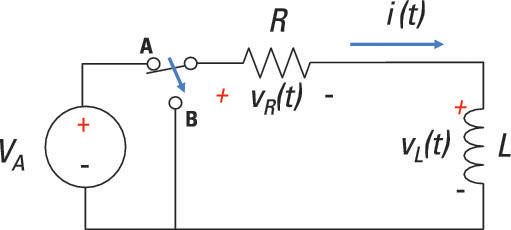
Para este circuito, tiene la siguiente ecuación KVL:
vR(t) + vL(t) = 0
A continuación, la formulación de la ecuación elemento (o i-v característica) para cada dispositivo. El uso de la ley de Ohm para describir la tensión en la resistencia, tiene la siguiente relación:
vR(t) = iL(t) R
Elemento de la ecuación de El inductor es
Sustituyendo las ecuaciones de los elementos, vR(t) y vL(t), en la ecuación KVL le da la ecuación diferencial de primer orden deseado:
En el Paso 2: Aplicar la transformada de Laplace de la ecuación diferencial:
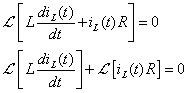
La ecuación anterior se utiliza la propiedad de linealidad que dice que usted puede tomar la transformada de Laplace de cada término. Para el primer término en el lado izquierdo de la ecuación, se utiliza la propiedad de diferenciación:
Utiliza esta ecuación yoL(s) = # 8466-[yoL(t)], y yo0 es la corriente inicial que fluye a través del inductor.
La transformada de Laplace de la ecuación diferencial se convierte en
yoL(s) R + L [sIL(s) - I0] = 0
Resolver yoL(s):
Para una condición inicial dada, esta ecuación proporciona la solución yoL(t) a la ecuación original diferencial de primer orden. Sólo tiene que realizar una transformada inversa de Laplace de yoL(s) - o buscar la transformación correspondiente par en esta tabla - para volver al dominio del tiempo.
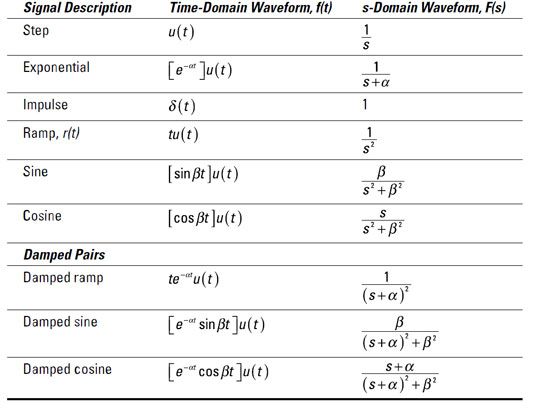
La ecuación anterior tiene una forma exponencial para la transformada de Laplace par. Usted terminará con la siguiente solución:
El resultado muestra el paso del tiempo t tiende a infinito, la corriente inicial inductor finalmente muere a cero después de un largo período de tiempo - unos 5 constantes de tiempo (L / R).
-
Ecuaciones diferenciales libro para los maniquíes - ¿Cómo decirle a una ecuación diferencial de otro
-
Resolución de ecuaciones diferenciales mediante transformada de Laplace soluciones -
Comprobación de soluciones de ecuaciones diferenciales -
Definición de ecuaciones diferenciales homogéneas y no homogéneas -
Analizar un circuito de primer orden rc usando métodos LaPlace
Analizar un circuito RC serie usando una ecuación diferencial Un circuito en serie RC de primer orden tiene una resistencia (o de la red de resistencias) y un condensador conectado en serie. De primer orden circuitos RC se pueden analizar utilizando ecuaciones diferenciales de primer orden. Mediante el…
Analizar un circuito RLC utilizando métodos LaPlace El uso de la transformada de Laplace como parte de su análisis de circuitos le proporciona una predicción de respuesta del circuito. Analizar los polos de la transformada de Laplace para obtener una idea general del comportamiento de salida. Polos…
Describir los circuitos de segundo orden con ecuaciones diferenciales de segundo orden Si usted puede utilizar una ecuación diferencial de segundo orden para describir el circuito que está viendo, entonces usted está tratando con un circuito de segundo orden. Circuitos que incluyen un inductor, condensador y resistencia conectada…
Encuentra la respuesta de estado cero de un circuito paralelo rl Un primer orden circuito en paralelo RL tiene una resistencia (o de la red de resistencias) y un único inductor. Circuitos de primer orden pueden ser analizadas usando las ecuaciones diferenciales de primer orden. Mediante el análisis de un…
Transformadas de Laplace y análisis de circuitos s-dominio Transformada de Laplace métodos pueden ser empleados para estudiar circuitos en el s-dominio. Técnicas de Laplace convierten circuitos con señales de tensión y corriente que cambian con el tiempo a la s-dominio para que pueda analizar la acción…
Análisis de S-dominio: la comprensión de polos y ceros de f (s) Transformadas de Laplace se pueden utilizar para predecir el comportamiento de un circuito. La transformada de Laplace toma una función de dominio de tiempo f (t), y la transforma en la función F (s) en el s-dominio. Puede ver las transformadas de…
Cómo utilizar pylab diferenciales LCC y ecuaciones en diferencias Herramientas informáticas juegan un papel importante en las señales y los sistemas modernos de análisis y diseño. LCC diferencial y ecuaciones en diferencias son una parte fundamental de los sistemas simples y de alta complejidad.…
Analizar un circuito RL paralelo usando una ecuación diferencial Un primer orden circuito en paralelo RL tiene una resistencia (o de la red de resistencias) y un único inductor. Circuitos de primer orden pueden ser analizadas usando las ecuaciones diferenciales de primer orden. Mediante el análisis de un…
Analizar un segundo orden circuito paralelo RLC utilizando la dualidad Circuitos RLC de segundo orden tienen una resistencia, inductor, y el condensador conectado en serie o en paralelo. Para analizar un circuito paralelo de segundo orden, se sigue el mismo proceso para el análisis de un circuito serie RLC.Aquí hay…
Encuentra la respuesta total de un circuito paralelo rl Después de encontrar la respuesta a entrada cero y la respuesta de estado cero de un circuito RL en paralelo, usted puede encontrar fácilmente la respuesta total del circuito. Recuerde que un circuito RL paralelo primer orden tiene una resistencia…
Encuentra la respuesta total de un circuito RC serie Después de encontrar la respuesta a entrada cero y la respuesta de estado cero de un circuito en serie RC, usted puede encontrar fácilmente la respuesta total del circuito. Recuerde que un circuito en serie RC de primer orden tiene una resistencia…
Encuentra las respuestas de entrada cero y por el estado cero de un circuito RC serie Para encontrar la respuesta total de un circuito RC en serie, es necesario encontrar la respuesta a entrada cero y la respuesta de estado cero y luego sumarlos. Un circuito en serie RC de primer orden tiene una resistencia (o de la red de…