Análisis de S-dominio: la comprensión de polos y ceros de f (s)

Transformadas de Laplace se pueden utilizar para predecir el comportamiento de un circuito. La transformada de Laplace toma una función de dominio de tiempo f (t), y la transforma en la función F (s) en el s-dominio. Puede ver las transformadas de Laplace F (s) como cocientes de polinomios en la s-dominio. Si usted encuentra las raíces reales y complejas (polos) de estos polinomios, se puede obtener una idea general de lo que la forma de onda f (t) se verá así.

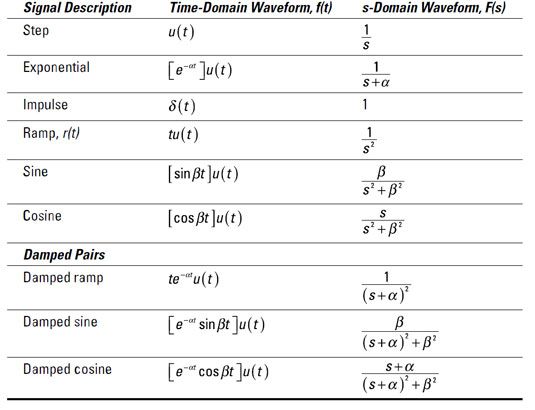
Por ejemplo, como se muestra en esta tabla, si las raíces son reales, entonces la forma de onda es exponencial. Si son imaginarios, entonces es una combinación de senos y cosenos. Y si son complejos, entonces es una sinusoide de amortiguación.

Las raíces del polinomio en el numerador de F (s) son ceros, y las raíces del polinomio del denominador son polos. Los polos resultan en F (s) volar hasta el infinito o ser indefinido - son las asíntotas verticales y agujeros en su gráfico.

Por lo general, se crea un polo-cero diagrama trazando las raíces en el s-plano (real y ejes imaginarios). El diagrama de polos y ceros proporciona una visión geométrica y la interpretación general del comportamiento del circuito.

Por ejemplo, considere la siguiente transformada de Laplace F (s):

Esta expresión es una relación de dos polinomios en s. Factoring el numerador y el denominador le da la siguiente descripción de Laplace F (s):

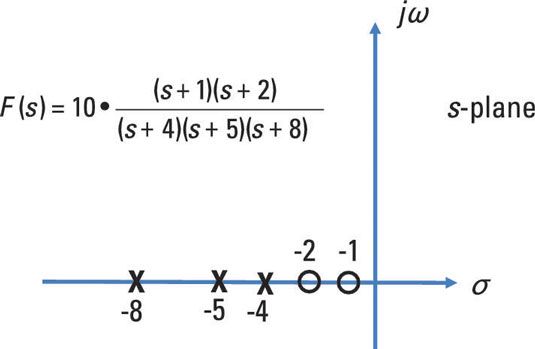
los ceros, o raíces del numerador, son s = -1, -2. los polos, o las raíces del denominador, son s = -4, -5, -8.

Ambos polos y ceros se llaman colectivamente frecuencias críticas porque el comportamiento de salida loca ocurre cuando F (s) tiende a cero o explota. Mediante la combinación de los polos y ceros, usted tiene el siguiente conjunto de frecuencias críticas: {-1, -2, -4, -5, -8}.

Este diagrama de polos y ceros traza estas frecuencias críticas en el s-avión, proporcionando una vista geométrica de comportamiento del circuito. En este diagrama de polos y ceros, X denota polos y O denota los ceros.

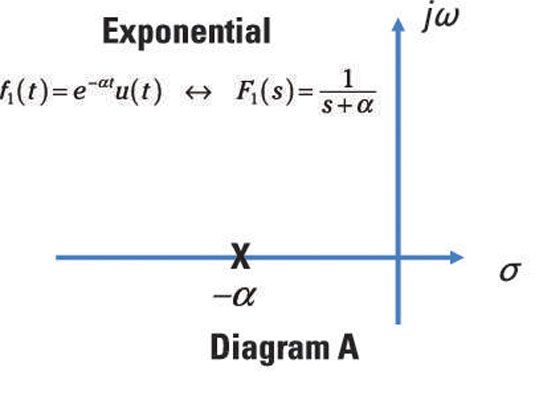
Estos son algunos ejemplos de los polos y ceros de las transformadas de Laplace, F (s). Por ejemplo, la transformada de Laplace F₁(s) para una amortiguación exponencial tiene un par de transformadas como sigue:

El exponencial transformar F₁(s) tiene un polo en s = -alfa- y no hay ceros. Aquí, se ve el polo de F₁(s) representada en el eje real negativo en el medio plano izquierdo.

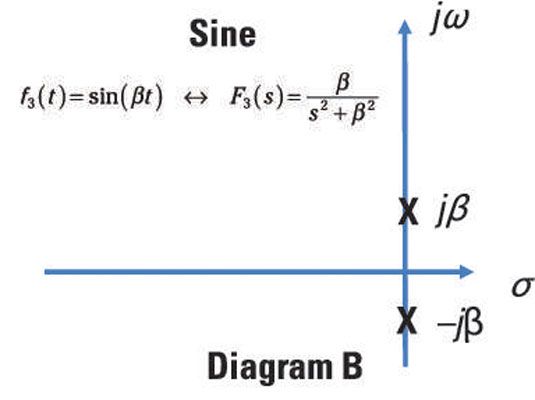
La función seno tiene la siguiente transformada de Laplace par:

La ecuación anterior no tiene ceros y polos imaginarios dos - en s = + jbeta y s = -jbeta. Polos imaginarios siempre vienen en pares. Estos dos polos están no amortiguado, porque cada vez que los polos se encuentran en el eje imaginario jomega-, la funcion f (t) oscilará para siempre, sin nada a la humedad hacia fuera. Aquí, se ve una parcela del diagrama de polos y ceros de una función sinusoidal.

Una función de rampa tiene la siguiente transformada de Laplace par:

La función de rampa tiene dobles polos en el origen (s = 0) y no tiene ceros.

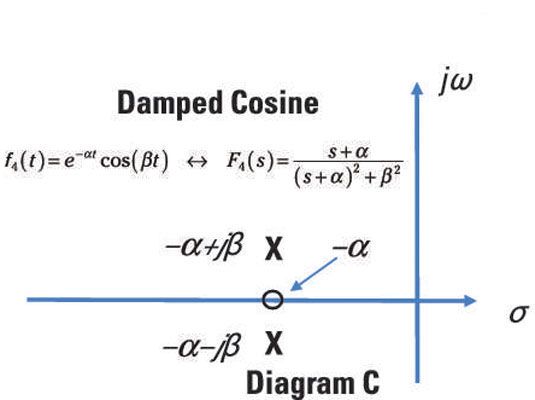
Aquí está un par de transformadas para una señal coseno amortiguado:

La ecuación anterior tiene dos polos complejos en s = alfa- + jbeta y s = alfa- - jbeta y uno cero en s = -alfa-.

Polos complejos, como polos imaginarios, siempre vienen en pares. Siempre que tenga un complejo par de polos, la función tiene oscilaciones que serán amortiguadas a cero en el tiempo - no van a durar para siempre. El comportamiento sinusoidal amortiguada consiste en una combinación de una exponencial (debido a la parte real alfa- del número complejo) y el oscilador sinusoidal (debido a la parte imaginaria beta del número complejo).

Aquí, usted ve representado el diagrama de polos y ceros de un coseno amortiguado.