Señales y sistemas del mundo real caso: diseño de filtros analógicos con un toque

Que le den la tarea de diseñar un análogo (en tiempo continuo) filtrar para cumplir con las especificaciones de respuesta de amplitud que se muestran. También es necesario para encontrar la respuesta al escalón del filtro, determinar el valor de la superación de pico, y el tiempo en que se produce el rebasamiento de pico.

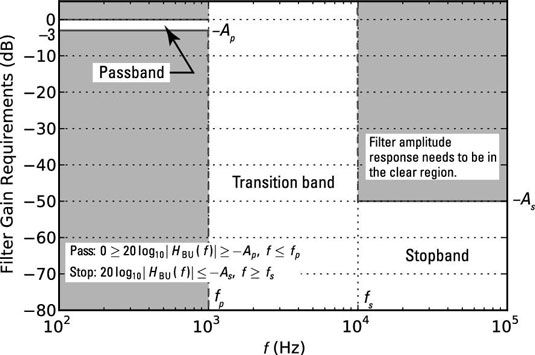
El objetivo del diseño de filtro es para la magnitud de respuesta de frecuencia en dB (20log₁₀|H(F) |) Pase a través de la región sombreada de la figura a medida que aumenta la frecuencia. Los requisitos de diseño se reducen a las frecuencias de paso de banda y banda de detención críticos F_p y F_s Hz y los niveles de atenuación de banda de paso y la banda de parada LA_p y LA_s dB.

Además, la característica de respuesta es estar Butterworth, lo que significa que la función de respuesta y el sistema de magnitud filtro de tomar este formulario:

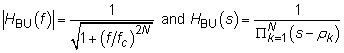
Aquí, N es el orden del filtro, F_c es la banda de paso 3 dB frecuencia de corte del filtro, y los polos, situados en un semicírculo es la izquierda; media s-avión, están dadas por

Este problema requiere trabajar en el dominio de la frecuencia, el dominio del tiempo, y tal vez la s-dominio, dependiendo del enfoque de solución que elija.

De los requisitos, la respuesta de frecuencia del filtro tiene la ganancia unitaria (0 dB) en la banda de paso. La respuesta al escalón (una caracterización de dominio de tiempo) del filtro Butterworth se conoce a rebasar la unidad antes de asentarse finalmente a la unidad como

Para diseñar el filtro, puede utilizar uno de los dos enfoques:

1. Trabajar una solución a mano, usando la respuesta de frecuencia magnitud Butterworth |H_BU(F) | y la función del sistema, H_BU(s).

2. Utilice las capacidades de diseño de filtro de la SciPy señal paquete.

Encontrar el orden del filtro y 3 dB Frecuencia de corte

Siga estos pasos para diseñar el filtro utilizando Python y SciPy que ver el número real crujido:

1. Encontrar N y F_c para cumplir con los requisitos de respuesta de magnitud.

   Utilice la función SciPy N, wc = signal.buttord (wp, ws, Ap, As, analógica = 1) y entrar en los requisitos de diseño de filtros, donde wp y ws son la banda de paso y la banda de detención frecuencias críticas en rad / s y Ap y Como son los niveles de paso de banda y banda de detención de atenuación (ambos conjuntos de cifras provienen de la figura anterior). La función devuelve el orden del filtro N y la frecuencia de corte WC en rad / s.

2. Sintetizar el filtro - encontrar el {b_k} Y {la_k} Coeficientes de la ecuación diferencial de LCC que realiza el sistema deseado.

   Si la búsqueda de elementos de circuito es el final del juego, puede ir allí de inmediato, utilizando fórmulas de síntesis de circuitos. Llame a la función SciPy b, a = signal.butter (N, wc, analógica = 1) con el orden del filtro y la frecuencia de corte, y devuelve los coeficientes de filtro en arrays b y la.

3. Encuentra la respuesta al escalón en forma matemática exacta o por medio de la simulación.

Aquí es cómo utilizar las herramientas de Python con los requisitos de diseño dados y luego verificar el trabajo por el trazado de la respuesta de frecuencia como una superposición. Nota: Usted puede hacer lo mismo en MATLAB con casi la misma sintaxis.

En [379]: N, wc = signal.buttord (2 * pi * 1e3,2 * pi * 10e3,3.0,50, analógica = 1) # find orden del filtro NIn [380]: N # filtro orderOut [380]: 3En [381]: Wc frec # corte en rad / sOut [381]: 9222.4701630595955In [382]: B, a = signal.butter (N, wc, analógica = 1) # get coeffs.In [383]: Combate [383]: Array ([7.84407571e + 11 + 0.j]) En [384]: Real (a) Sale [384]: Array ([1.00000000e + 00, + 1.84449403e 04,1.70107912e + 08,7.84407571e + 11])

Los resultados de la línea [379] te dicen que el orden del filtro requerido es N = 3 y la frecuencia de corte del filtro es requerido

Los conjuntos de coeficientes de filtro también se incluyen en los resultados.

Utilizar el real () función para visualizar de forma segura la parte real de la matriz de coeficientes la porque sabes que los coeficientes son reales. ¿Cómo? Los postes, las raíces del denominador de H_BU(s), Son reales o ocurren en pares complejos conjugados, lo que garantiza que el polinomio denominador tiene coeficientes reales cuando se multiplica a cabo. Las pequeñas partes imaginarias se deben a errores numéricos de precisión.

Comprobación de la respuesta de frecuencia diseño final

Para comprobar el diseño, utilice la receta de respuesta de frecuencia.

En [386]: F = logspace (2,5,500) axisIn # registro de frecuencia [387]: W, H = signal.freqs (b, a, 2 * pi * f) En [388]: Semilogx (f, 20 * log10 (abs (H)), 'g')

La figura muestra la gráfica de la respuesta de magnitud diseño final, junto con los requisitos de diseño originales.

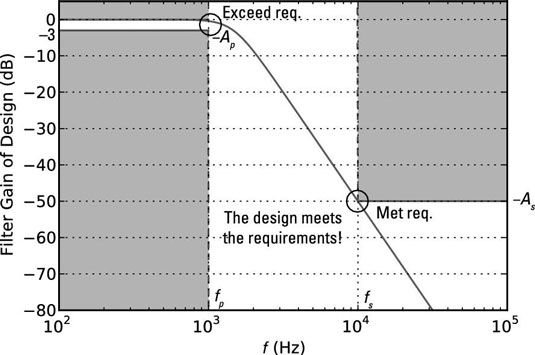
Encontrar la respuesta al escalón de los coeficientes del filtro

El enfoque más elegante a la búsqueda de la respuesta al escalón de los coeficientes del filtro es encontrar

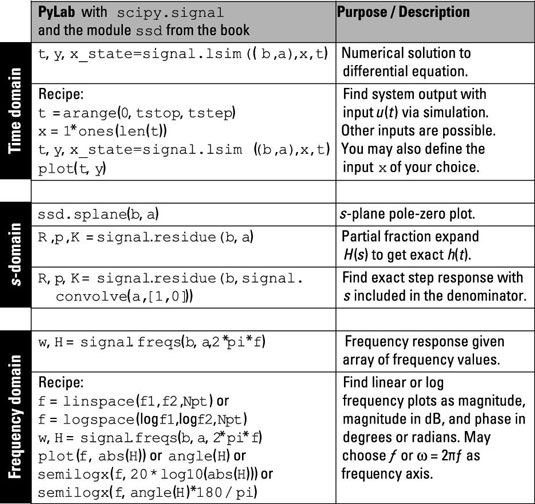
los s-la sección de dominio de la figura se indica cómo completar la expansión en fracciones parciales (PFE) numéricamente. Dispone de las matrices de coeficientes para H(s), Por lo que todo lo que tiene que hacer es multiplicar el polinomio denominador por s. Usted puede hacer esto a mano o puede utilizar una relación entre los coeficientes polinómicos y secuencia de convolución.

Al multiplicar dos polinomios, las matrices de coeficientes para cada polinomio se convolucionados, como en la secuencia de convolución.

Aquí, usted trabaja a través del problema, utilizando signal.convolve para llevar a cabo la multiplicación polinomio en el denominador. Para convencerte de que esto realmente funciona, considere la posibilidad de multiplicación de las siguientes dos polinomios:

(X² + X + 1) (X + 1) = X³ + 2X² + 2X + 1

Si convolve los coeficientes conjuntos [1, 1, 1] y [1, 1] como matrices en Python, se obtiene esta salida:

En [418]: Signal.convolve ([1,1,1], [1,1]) Sale [418]: Array ([1, 2, 2, 1])

Esto está de acuerdo con el cálculo manual. Para encontrar el PFE, conecte los coeficientes de las matrices b y convolve (a, [1,0]) dentro R, P, K = residuo (b, a). Los coeficientes de [1, 0] que correspondan a las s-polinomio de dominio s + 0.

En [420]: R, P, K = signal.residue (b, signal.convolve ([1,0], a)) En [421]: R # (residuos) rayar pequeña errorsOut numérica [421]: array ([1.0000e + 00 + 2.3343e-16j, # residuo 0, parte imag 0-1.0000e + 00 + 1.0695e-15j, # residuo 1, parte imag 01.08935e-15 -5.7735e-01J, # residuos 2, parte real 01.6081e-15 + 5.7735e-01J]) # residuo 3, parte real 0cm [422]: P # (polos) Sale [422]: array ([0.0000 + 0.0000e + 00j, # polo 0-9222,4702 -1.5454e-12j, # 1 polo, imag parte 0-4611,2351 -7.9869e + 03J, # polo 2-4611,2351 + 7.9869e + 03J]) # polo 3En [423]: K # (de la división larga) Sale [423]: Array ([0 + 0.j]) # adecuada racional, así que no hay términos

Tienes cuatro polos: dos reales y un par complejo conjugado - un poco de un lío para trabajar a través de, pero es factible. Consulte el par transformar

para calcular la transformada inversa para los cuatro términos.

Para los polos conjugados, los residuos también son conjugados. Esta propiedad siempre se mantiene.

Usted puede escribir la transformada inversa de los términos de polos conjugado como senos y cosenos, utilizando la fórmula de Euler y la cancelación de las partes imaginarias delante del coseno y partes reales delante del seno:

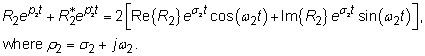
Poniendo todo junto, se obtiene y_paso(t) = u(t) - e^-9,222.47tu(t) -2 X 0,5774e^-4,611.74tsin (7,986.89t)u(t). Tener esta forma es bonita, pero todavía se necesita para encontrar la máxima función para t > 0 y la ubicación máxima. Para ello, trazar la función y observar el máximo.

Un enfoque más directo es el uso de la simulación a través de signal.lsim y la receta de dominio de tiempo. La entrada del sistema es un paso, por lo que la salida de la simulación será la respuesta al escalón. A partir de la respuesta al escalón simulado, se puede calcular el rebasamiento máximo numéricamente y verlo en una parcela. El código de línea de comandos es IPython

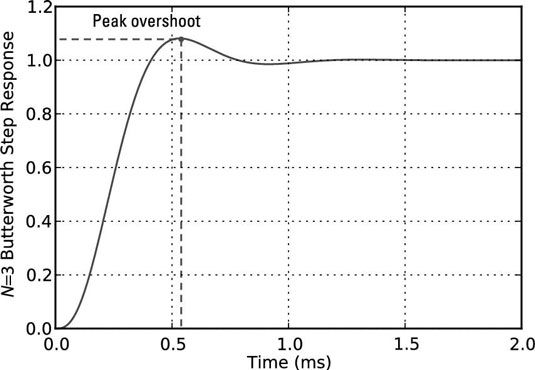
En [425]: T = arange (0,0.002,1e-6) # paso menos de tiempo más pequeño Constantin [426]: T, ys, x_state = signal.lsim ((b, a), los (len (t)), t) En [428]: Plot (t * 1E3, ys)

Usando el tiempo t matriz y la matriz de respuesta de paso ys, puede utilizar la max () y encontrar() funciones para completar la tarea:

En [436]: Max (real (ys)) # reales para borrar num. errorsOut [436]: 1,0814651457627822 # máximo sobreimpulso is8.14% En [437]: Encontrar (reales (ys) == max (reales (ys))) de salida [437]: Array ([534]) pico # hallazgo sea en el índice 534In [439]: T [534] * 1E3 # tiempo en el índice 534 en msOut [439]: 0,5339