Cómo utilizar pylab diferenciales LCC y ecuaciones en diferencias

Herramientas informáticas juegan un papel importante en las señales y los sistemas modernos de análisis y diseño. LCC diferencial y ecuaciones en diferencias son una parte fundamental de los sistemas simples y de alta complejidad. Afortunadamente, las herramientas de software actuales hacen que sea posible trabajar a través de dominios con estas ecuaciones LCC sin demasiado dolor.

LCC diferenciales y diferencia ecuaciones están completamente caracterizados por el {la_k} Y {b_k} Conjuntos de coeficientes. Puede utilizar herramientas como Pylab con el SciPy señal paquete para diseñar filtros de alto rendimiento, en particular en el dominio de tiempo discreto. Las funciones de diseño de filtro de señal le dará la {la_k} Y {b_k} Coeficientes en respuesta a los requisitos de diseño que de entrada. A continuación, puede utilizar los diseños de filtros en la simulación de sistemas más grandes.

Tiempo continuo

Tres representaciones del sistema de ecuación diferencial LCC son el tiempo, la frecuencia y s-dominios, y los mismos conjuntos de coeficientes, {b_k} Y {la_k}, Existir en las tres representaciones. Aquí están las relaciones de entrada y salida correspondientes en estos dominios:

• Dominio del tiempo (de la ecuación diferencial):

• Dominio del tiempo (de respuesta de impulso):

• Dominio de la frecuencia:

• s-dominio:

En la segunda línea de la ecuación diferencial, la respuesta de impulso, h(t), Junto con la integral de convolución producir la salida, y(t), A partir de la entrada, X(t). En la tercera línea, el teorema de convolución para transformadas de Fourier produce el espectro de salida, Y(F), Como el producto del espectro de entrada, X(F), Y la respuesta de frecuencia, H(F) - Que es la transformada de Fourier de la respuesta al impulso.

En la cuarta línea, el teorema de convolución de transformadas de Laplace produce la s-salida en el dominio, Y(s), Como el producto de la entrada, X(s), Y la función del sistema, H(s) - Que es la transformada de Laplace de la respuesta de impulso.

Los figurehighlights las funciones clave en PyLab y la ssd.py módulo de código que puede utilizar para trabajar a través de los dominios de tiempo continuo. Recuerde, estas funciones están en el nivel superior. Usted puede integrar muchas funciones de nivel inferior (como las matemáticas, la manipulación de matrices y funciones de la biblioteca de trazado) con estas funciones de alto nivel para llevar a cabo tareas de análisis específicos.

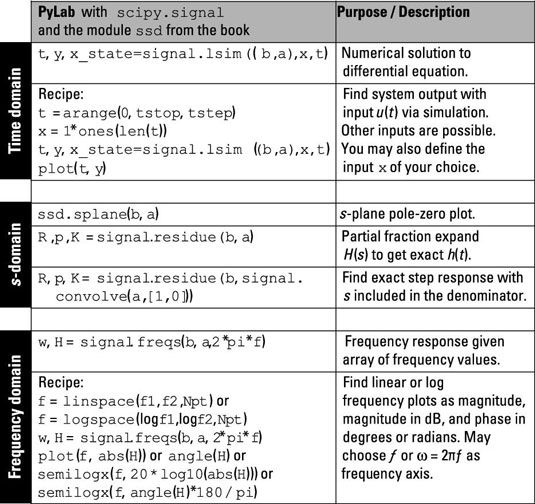
Esto es lo que puede encontrar:

• Las filas de dominio de tiempo muestran una receta para resolver numéricamente la ecuación diferencial mediante el uso de signal.lsim ((b, a), x, t) para una entrada función escalón. Los arrays b y la corresponden a los conjuntos de coeficientes {b_k} Y {la_k}. Son posibles señales de entrada de su propia elección, también. La simulación de dominio de tiempo le permite caracterizar el comportamiento de un sistema en el nivel de forma de onda real.

• en el s-filas de dominio, encuentra la parcela polos cero de la función del sistema H(s) mediante el uso ssd.splane (b, a). También encuentre la manera de resolver la expansión en fracciones parciales (PFE) de H(s) Y H(s) /s para obtener una representación matemática de la respuesta de impulso o la respuesta al escalón.

• La sección de dominio de la frecuencia ofrece una receta para el trazado de la respuesta de frecuencia del sistema mediante el uso de signal.freqs (b, a, 2 * pi * f). Las opciones incluyen una la respuesta de fase en grados lineal o eje de frecuencia de registro, la magnitud de respuesta de frecuencia, y.

Tiempo discreto

Al igual que para los sistemas de ecuaciones diferenciales que se describen en la sección anterior, el sistema de ecuaciones diferencia LCC tiene tres representaciones: el tiempo, la frecuencia y zdominios, y los mismos conjuntos de coeficientes, {b_k} Y {la_k}, Existir en las tres representaciones. Aquí están las relaciones de entrada y salida correspondientes en estos dominios:

• Dominio del tiempo (de ecuación en diferencias):

• Dominio del tiempo (de respuesta de impulso):

• Dominio de la frecuencia:

• z-dominio:

En la segunda línea de la ecuación de diferencia, la respuesta de impulso, h[n], Junto con la suma de convolución producir la salida, y[n], Forman la entrada, X[n]. En la tercera línea, el teorema de convolución para transformadas de Fourier produce el espectro de salida,

que es el tiempo-discreto transformada de Fourier de la respuesta al impulso.

En la cuarta línea, el teorema de convolución para ztransformadas produce la zsalida en el dominio, Y(z), Como el producto de la entrada, X(z), Y la función del sistema, H(z), Cuál es el ztransformada de la respuesta de impulso.

La cifra pone de relieve las funciones clave en PyLab y la costumbre ssd.py módulo de código que puede utilizar para trabajar a través de los dominios de tiempo discreto.

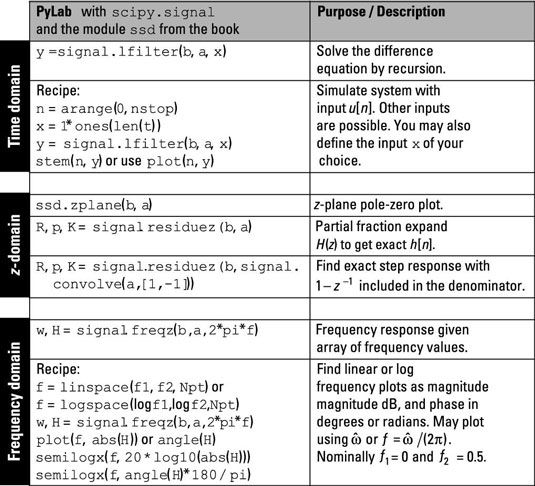
• En las filas de dominio de tiempo, a resolver la ecuación diferencia exactamente, utilizando signal.lfilter (b, a, x).

• en el zfilas de dominio, usted puede encontrar la trama polos cero de la función del sistema H(z), usando ssd.zplane (b, a), y la expansión en fracciones parciales, usando signal.residuez en lugar de signal.residue.

• Las filas de dominio de frecuencia muestran cómo encontrar la respuesta en frecuencia de un sistema de tiempo discreto con signal.freqz (b, a, 2 * pi * f), dónde F es la variable de frecuencia