Determinar dominio y el rango de una función trigonométrica
Una función consiste en una regla que se aplica a los valores de entrada. El resultado es un único valor de salida. Generalmente, usted puede utilizar un gran número de valores de entrada, y son parte de la dominio
de la función. Los valores de salida constituyen el alcance de la función.Dominio de una función trigonométrica
El dominio de una función se compone de todos los valores que se pueden utilizar como entrada a la regla de la función. El dominio es otra de las características de esa función, porque diferentes funciones tienen diferentes números que usted puede entrar y tener las salidas tienen ningún sentido.
es una función cuyo dominio no puede contener todos los números negativos, debido a que la raíz cuadrada de un número negativo no es un número real.
La siguiente función tiene un dominio que no se puede incluir el número -3:
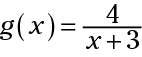
Cualquier otro número real está bien, pero no -3, porque poner un -3 por X hace el denominador igual a 0, y no se puede dividir por 0. (. Una fracción con un 0 en el denominador representa un número que no existe) Con funciones trigonométricas, el dominio (valores de entrada) es medidas de los ángulos - ya sea en grados o radianes.
Algunas de las funciones trigonométricas tienen restricciones en sus dominios, también. Por ejemplo, la función tangente tiene un dominio que no se puede incluir de 90 grados o 270 grados, entre los muchos otros valores restringidos.
Rango de una función trigonométrica
El rango de una función consiste en todos sus valores de salida - el número que se obtiene al introducir números de dominio en la función y realizar las operaciones de función en ellos. A veces, una serie puede ser todos los posibles números reales - no tiene límite.
Esta situación ocurre en una función tal como h(X) = 3X + 2. En esta ecuación, tanto el dominio y el rango son ilimitadas. Usted puede poner en cualquier número real, y se puede obtener una potencia de cualquier número real que puedas imaginar. Los rangos pueden llegar a ser restringida, sin embargo.
Por ejemplo, la función de k(X) = X2 + 6 siempre tendrá resultados que son o bien el número 6 o algún número positivo mayor que 6. Nunca se puede obtener un número negativo o un número inferior a 6 como una salida. Los rangos de algunas funciones trigonométricas están restringidas, también. Por ejemplo, la salida de la función seno nunca excede de 1 o va más baja que -1.
-
Roles de los controladores de dominio de Active Directory -
Funciones del alfabeto en el álgebra -
Conceptos básicos de función para pre-cálculo -
Cómo ajustar el dominio y el rango de funciones combinadas -
¿Cómo encontrar extremos absolutos sobre todo el dominio de una función -
Cómo graficar una función coseno
Cómo graficar una función cotangente Los gráficos de los padres de tangente y cotangente son comparables, ya que ambos tienen asíntotas y X-intercepta. Las únicas diferencias se pueden ver son los valores de theta donde las asíntotas y X-se producen intersecciones. Usted puede…
Cómo graficar una función tangente La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…
Cómo graficar una función seno Sabiendo cómo graficar funciones trigonométricas le permite medir el movimiento de los objetos que se mueven hacia atrás y hacia adelante o hacia arriba y hacia abajo en un intervalo regular, como péndulos. Funciones seno son formas perfectas de…
Cómo reflejar la gráfica de una función Reflexiones tomar una función madre y proporcionar una imagen especular de la vuelta, ya sea una línea horizontal o vertical. Te encontrarás con dos tipos de reflexiones:Un número negativo se multiplica toda la función La negativa fuera de la…
Una tabla rápida para las tres funciones trigonométricas recíprocas Usted sabe que las funciones recíprocas tienen valores que son recíprocos, o voltea, de los valores de sus respectivas funciones. El recíproco de seno es cosecante, por lo que cada valor de la función para la cosecante es el recíproco del seno…
Dominios y rangos de funciones trigonométricas El dominio de una función se compone de todos los valores de entrada que una función puede manejar - la manera que la función está definida. Por supuesto, usted desea conseguir valores de salida (que conforman la gama) cuando introduce valores…
Gama de funciones seno y coseno de dominio y Las funciones seno y coseno son únicos en el mundo de las funciones trigonométricas, porque sus relaciones siempre tienen un valor. No importa desde qué ángulo lo de entrada, se obtiene una salida resultante. El valor que se obtiene puede ser 0,…
Funciones trigonométricas secantes gama de Dominio y cosecante y Las funciones cosecante y secante están estrechamente ligados a seno y coseno, porque son los respectivos recíprocos. En referencia al plano de coordenadas, cosecante es r/y, y secante es r/X. El valor de r es la longitud de la hipotenusa de un…
Gama de funciones trigonométricas tangente y cotangente Dominio y La tangente y cotangente están relacionadas no sólo por el hecho de que son recíprocos, sino también por el comportamiento de sus rangos. En referencia al plano de coordenadas, tangente es y/X, y cotangente es X/y. Los dominios de ambas…
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
Múltiplos gráfica de la función tangente En trigonometría, valores tangentes van desde menos infinito hasta el infinito positivo. Así que cuando usted multiplica toda la función tangente de un número, esto es lo que sucede: Si se multiplica por un número mayor que 1, la función se…
¿Cómo encontrar una función trigonométrica inversa Las funciones trigonométricas inversas todos tienen, pero sólo en condiciones especiales - usted tiene que restringir los valores de dominio. No todas las funciones tienen inversos, y no todos los inversos son fáciles de determinar. Aquí es un…