Cómo ajustar el dominio y el rango de funciones combinadas
Cuando comience la combinación de funciones (como la adición de un polinomio y una raíz cuadrada, por ejemplo), el dominio de la nueva función combinada se ve afectada. Lo mismo puede decirse de la gama de un combinado funcionalidad la nueva función estará basado en la restricción (s) de las funciones originales.
Conteúdo
El dominio se ve afectada cuando se combinan las funciones con la división porque las variables terminan en el denominador de la fracción. Cuando esto sucede, es necesario especificar los valores en el dominio para el que el cociente de la nueva función no está definido. Los valores no definidos se llaman también la valor excluidos para el dominio. Si F(X) = X2 - 6X + 1 y g(X) = 3X2 - 10, si nos fijamos en
esta fracción ha excluido a los valores ya F(X) Es una ecuación de segundo grado con raíces reales. Las raíces de F(X) son
por lo que se excluyen estos valores.
Desafortunadamente, no hay un método infalible para encontrar el dominio y rango de una función combinada. El dominio y el rango a encontrar una función combinada dependen del dominio y el rango de cada una de las funciones originales de forma individual. Para tener una idea del dominio y el rango de la función combinada, sólo tiene que descomponen el problema y mirar a los dominios y rangos individuales.
Encontrar el dominio de una composición de funciones
Dadas dos funciones, F(X) Y g(X), Se supone que tiene que encontrar el dominio de la nueva función combinada F(g(X)). Para ello, es necesario encontrar el dominio de cada función individual primero. Si
y g(X) = 25 - X2, aquí es cómo encontrar el dominio de la función compuesta F(g(X)):
Encontrar el dominio de F(X).
Porque usted no puede raíz cuadrada de un número negativo, el dominio de F tiene que ser todos los números no negativos. Matemáticamente, se escribe esto como
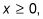
o en la notación de intervalo,
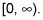
Encontrar el dominio de g(X).
Debido a que esta ecuación es un polinomio, su dominio es todos los números reales, o
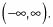
Encuentre el dominio de la función combinada.
Cuando se le preguntó específicamente para observar la función compuesta F(g(X)), tenga en cuenta que g esta adentro f. Usted todavía está tratando con una función de raíz cuadrada, lo que significa que todavía se aplican todas las reglas para funciones de raíz cuadrada. Así que la nueva radicando de la función compuesta tiene que ser no negativo:
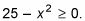
Resolver esta desigualdad cuadrática le da
que constituyen el dominio de la función compuesta:
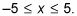
Encontrar el rango de una composición de funciones
Para encontrar el rango de la misma función compuesta, también debe considerar el rango de ambas funciones originales primeros:
Encontrar el rango de F(X).
Una función de raíz cuadrada siempre da respuestas no negativos, por lo que su rango es
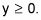
Encontrar el rango de g(X).
Esta función es un polinomio de grado par (en concreto, una cuadrática) y polinomios incluso grados siempre tienen un valor mínimo o máximo. Cuanto más alto es el grado en el polinomio, más difícil es encontrar el mínimo o el máximo. Debido a que esta función es " simplemente " un segundo grado, usted puede encontrar sus valores mínimos y máximos por localizar el vértice.
En primer lugar, vuelva a escribir la función como g(X) = -X2 + 25. Esta forma te dice que la función es una cuadrática transformado que se ha desplazado hasta el 25 y el vuelto del revés. Por lo tanto, la función nunca se pone más alta que en el 25 y dirección. El rango es
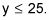
Encuentre el rango de la función compuesta F(g(X)).
La funcion g(X) Alcanza su máximo (25) cuando X = 0. Por lo tanto, la función compuesta también alcanza su máximo a X = 0:
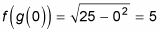
El rango de la función compuesta tiene que ser inferior a ese valor, o
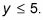
Recuerde que la gráfica de esta función combinada también depende de la gama de cada función individual. Debido a que la gama de g(X) Debe ser no negativo, por lo que debe ser el rango de la función compuesta. Esto se escribe como
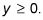
Por lo tanto, el rango de la función compuesta es
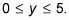
Si graficas esta función compuesta en su calculadora gráfica, se obtiene el semicírculo superior del radio de 5 que está centrada en el origen.
Cómo romper una composición de funciones LA composición de funciones es una función que actúa sobre otra. Piense en ello como poniendo una función dentro de la otra - F(g(X)), Por ejemplo, significa que se conecta el todo g(XFunción) en para todos X'pecado F(X). Para resolver este…
¿Cómo cambiar la amplitud, período, y la posición de un gráfico secante o cosecante Si tiene que cambiar la amplitud, período, y la posición de un gráfico secante o cosecante, su mejor apuesta es para graficar sus funciones recíprocas y transformarlos primero. Las funciones recíprocas, seno y el coseno, son más fáciles de…
¿Cómo encontrar extremos absolutos sobre todo el dominio de una función Una función de absoluta max y absoluta min sobre su todo el dominio son los valores más altos y más bajos (alturas) de la función de cualquier lugar que está definido. Cuando se tiene en cuenta todo el dominio de una función, una función…
Cómo graficar funciones parentales y troncos transformados Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…
Cómo graficar funciones parentales En matemáticas, se ve ciertos gráficos una y otra vez. Por esa razón, estas, funciones comunes originales se llaman gráficos de los padres, e incluyen gráficas de funciones cuadráticas, raíces cuadradas, valores absolutos, cúbicas y raíces…
Cómo graficar polinomios cuando las raíces son números imaginarios - una visión general En pre-cálculo y en el cálculo, ciertas funciones polinómicas tener raíces no reales además de raíces reales (y algunas de las funciones más complicadas tener todas raíces imaginarias). Cuando usted debe encontrar tanto, empezar por la…
Cómo invertir una función para encontrar su inversa Si te dan una función y debe encontrar su inversa, primero recordar que los lugares de dominio y de swap rango en las funciones. Literalmente, intercambias F(X) Y X en la ecuación original. Al realizar ese cambio, se llama a la nueva F(X) Por su…
Determinar dominio y el rango de una función trigonométrica Una función consiste en una regla que se aplica a los valores de entrada. El resultado es un único valor de salida. Generalmente, usted puede utilizar un gran número de valores de entrada, y son parte de la dominio de la función. Los valores de…
Dominios y rangos de funciones trigonométricas El dominio de una función se compone de todos los valores de entrada que una función puede manejar - la manera que la función está definida. Por supuesto, usted desea conseguir valores de salida (que conforman la gama) cuando introduce valores…
Gama de funciones trigonométricas tangente y cotangente Dominio y La tangente y cotangente están relacionadas no sólo por el hecho de que son recíprocos, sino también por el comportamiento de sus rangos. En referencia al plano de coordenadas, tangente es y/X, y cotangente es X/y. Los dominios de ambas…
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
¿Cómo encontrar una función trigonométrica inversa Las funciones trigonométricas inversas todos tienen, pero sólo en condiciones especiales - usted tiene que restringir los valores de dominio. No todas las funciones tienen inversos, y no todos los inversos son fáciles de determinar. Aquí es un…