¿Cómo cambiar la amplitud, período, y la posición de un gráfico secante o cosecante
Si tiene que cambiar la amplitud, período, y la posición de un gráfico secante o cosecante, su mejor apuesta es para graficar sus funciones recíprocas y transformarlos primero. Las funciones recíprocas, seno y el coseno, son más fáciles de gráfico porque no tienen tantas partes complejas (no hay asíntotas, básicamente). Si usted puede graficar los recíprocos primero, se puede hacer frente a las piezas más complicadas de las secantes / gráficos cosecant últimos.
Por ejemplo, echar un vistazo a la gráfica
Grafica la función recíproca transformado y = 1/4 cos X - 1.
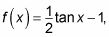
Mira la función recíproca de secante, que es el coseno. Pretend sólo por un poco de que está graficando
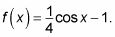
Siga todas las reglas para la gráfica coseno con el fin de terminar con un gráfico que se parece a la de la figura.
Dibuje las asíntotas de la función recíproca transformado.
Dondequiera que la gráfica transformada implica coseno atraviesa su eje sinusoidal, usted tiene una asíntota en el gráfico que implica secante. Usted ve que la gráfica coseno cruza el eje sinusoidal cuando X = Pi / 2 y 3pi / 2.
Descubra lo que la gráfica se ve como entre cada asíntota.
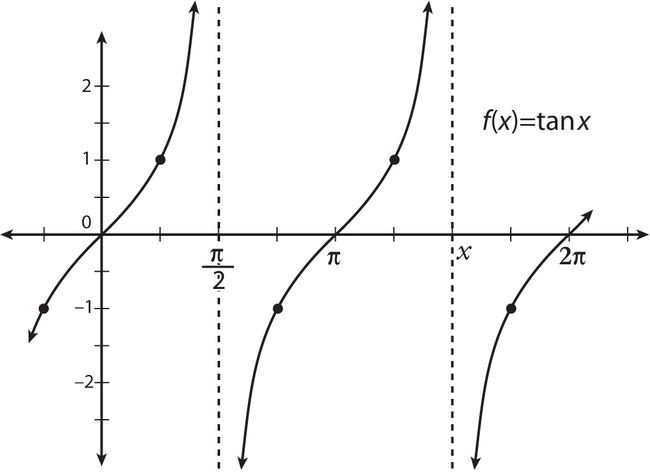
Ahora que ya ha identificado a las asíntotas, sólo tiene que averiguar lo que sucede en los intervalos entre ellos. El gráfico terminado,
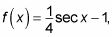
termina pareciéndose a la de la figura.
Indique el dominio y el rango de la función transformada.
Debido a que la nueva función transformada puede tener diferentes asíntotas que la función de los padres de la secante y puede ser desplazado hacia arriba o hacia abajo, es posible que se requiere para establecer el nuevo dominio y rango.
En este ejemplo,
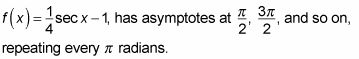
Por lo tanto, el dominio se restringe a no incluir estos valores y se escribe
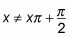
dónde X es un número entero. Además, la gama de esta función cambios porque la función de transformada es más corta que la función madre y se ha desplazado hacia abajo 2. La gama ha dos intervalos separados,
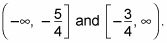
Puede representar gráficamente una transformación de la gráfica cosecante utilizando los mismos pasos que se utilizan al graficar la función secante, sólo que esta vez que utilice la función seno que te guíe.
La forma de la gráfica cosecant transformado debe ser muy similar a la gráfica de la secante, excepto las asíntotas están en diferentes lugares. Por esta razón, asegúrese de que está graficando con la ayuda de la gráfica de seno (para transformar la gráfica cosecante) y la función coseno (que le guiará para la gráfica secante).
Por ejemplo, gráfico El gráfico cosecante transformado
Grafica la función recíproca transformado.
Mira primero a la función
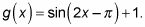
Las reglas para la transformación de una función seno le dicen a primer factor a cabo el 2 y obtener
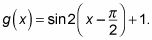
Se tiene una contracción horizontal de 2, un desplazamiento horizontal de
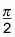
a la derecha, y un desplazamiento vertical de hasta 1. La figura muestra la gráfica sine transformado.
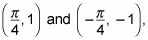
Dibuje las asíntotas de la función recíproca.
El eje sinusoidal que se ejecuta a través del medio de la función seno es la línea y = 1. Por lo tanto, existe una asíntota de la gráfica cosecante todas partes la función seno transformado cruza esta línea. Las asíntotas de la gráfica que involucran cosecante están en
Averiguar lo que sucede con el gráfico entre cada asíntota.
Puedes usar el gráfico transformada de la función seno para determinar dónde la gráfica cosecante es positivo y negativo. Debido a la gráfica de la función seno transformado es positivo en el medio
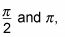
el gráfico cosecante es positivo también y se extiende hasta al conseguir más cerca de las asíntotas. Del mismo modo, debido a la gráfica de la función seno transformado es negativo en el medio
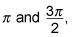
la cosecante también es negativo en este intervalo. Los suplentes del gráfico entre positivo y negativo en intervalos iguales para siempre en ambas direcciones.
La figura muestra la gráfica cosecante transformado.
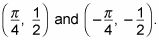
Indique el nuevo dominio y rango.
Al igual que con la gráfica transformada de la función secante, es posible que se le pida que indique el nuevo dominio y el rango de la función cosecante. El dominio de la función cosecant transformada es todos los valores de X a excepción de los valores que son asíntotas. De la gráfica, se puede ver que el dominio es todos los valores de X, dónde
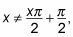
dónde X es un número entero. El rango de la función cosecante transformado también se divide en dos intervalos:
-
Representación gráfica de funciones trigonométricas en pre-cálculo -
¿Cómo cambiar la amplitud, período, y la posición de la tangente o gráfico cotangente -
¿Cómo combinar transformaciones con un gráfico de seno o coseno -
Cómo graficar una función cosecante -
Cómo graficar una función cotangente -
Cómo graficar una función secante
Cómo graficar una función tangente La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…
Cómo graficar funciones parentales y troncos transformados Quieres un poco de buenas noticias, de forma gratuita? Representación gráfica de funciones de los padres y los registros transformadas es muy fácil! Usted puede cambiar cualquier registro en una expresión exponencial, por lo que este paso es lo…
Cómo cambiar un gráfico seno o coseno en el plano de coordenadas El movimiento de un seno padre o gráfica coseno alrededor del plano de coordenadas es un tipo de transformación conocido como traducción o una cambio. Para este tipo de transformación, cada punto de la gráfica de los padres se trasladó a otro…
Una tabla rápida para las tres funciones trigonométricas recíprocas Usted sabe que las funciones recíprocas tienen valores que son recíprocos, o voltea, de los valores de sus respectivas funciones. El recíproco de seno es cosecante, por lo que cada valor de la función para la cosecante es el recíproco del seno…
Funciones trigonométricas secantes gama de Dominio y cosecante y Las funciones cosecante y secante están estrechamente ligados a seno y coseno, porque son los respectivos recíprocos. En referencia al plano de coordenadas, cosecante es r/y, y secante es r/X. El valor de r es la longitud de la hipotenusa de un…
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
Graficar una función seno usando amplitud La función seno y cualquiera de sus variaciones tienen dos características importantes: la amplitud y periodo de la curva. Puede determinar estas características examinado sea la gráfica de la función o su ecuación.los amplitud de la función…
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
Gráfico secante inversa y cosecante Las gráficas de las funciones cosecante secantes e inversas inversas tomarán un poco de explicación. En primer lugar, tener en cuenta que las funciones secante y cosecante no tienen valores de salida (y-valores) entre -1 y 1, por lo que un…
Grafica la función cosecante Una manera muy eficaz de graficar la función cosecante es hacer primero un boceto rápido de la función seno (su recíproco). Con el boceto de seno en su lugar, se puede dibujar las asíntotas de la función cosecante a través de la X-intercepta…
Variaciones Gráfico en una función secante La gráfica de una función secante es diferente de la cosecante de varias maneras, pero una de las maneras más evidentes es que la gráfica de la secante es simétrica con respecto al y-eje. El secante es un espejo de reflexión sobre ese eje.…
Graficar las asíntotas de una función secante Para graficar la curva de la secante, primero identificar las asíntotas determinando donde el recíproco de la secante - coseno - es igual a 0. Luego de realizar el boceto en ese recíproco, para que pueda determinar los puntos de inflexión y la…