Variaciones Gráfico en una función secante
La gráfica de una función secante es diferente de la cosecante de varias maneras, pero una de las maneras más evidentes es que la gráfica de la secante es simétrica con respecto al y-eje. El secante es un espejo de reflexión sobre ese eje. Puede utilizar esta propiedad para hacer algo interesante a la gráfica.
Las traducciones y multiplicaciones habituales afectan a la gráfica de la secante de la misma manera que lo hace las gráficas de las otras funciones trigonométricas. Si se multiplica la función por la sexta y añadir 2pi- a la variable de ángulo, como en la ecuación
usted consigue esta cifra.
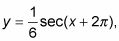
Comparado con y = Sec X, el gráfico de la figura anterior es mucho más cerca de la X-eje y parece estar aplanado entre las asíntotas. Estos cambios ocurren cuando se multiplica la función de un número entre 0 y 1. El punto de inflexión se encuentra todavía en el mismo lugar, pero el y-valor es mucho más cercano a 0.
La otra curiosidad es que las asíntotas no parecen ser diferentes. No son - y no deberían ser. Mediante la adición de 2pi- a la variable ángulo, cambias el gráfico 2pi- unidades a la izquierda. El gráfico realmente ha cambiado, pero no se puede decir, porque el nuevo gráfico que se encuentra por completo en el antiguo. Cuando el desplazamiento es igual al período de la función (la longitud del intervalo que le toma a los valores de la función para comenzar a repetir otra vez), el cambio no es aparente.
-
Representación gráfica de funciones trigonométricas en pre-cálculo -
¿Cómo cambiar la amplitud, período, y la posición de un gráfico secante o cosecante -
Cómo graficar una función cosecante -
Cómo graficar una función secante -
¿Cómo transformar horizontalmente gráficos padres -
¿Cómo traducir el gráfico de una función
Cómo utilizar el teorema de poder secante-secante Puede utilizar el secante-secante Poder teorema para resolver algunos problemas de círculo. Este teorema implica - ¿Estás sentado abajo - dos secantes! (Si usted está tratando de llegar a un nombre creativo para su hijo como Dweezil o Unidad…
Funciones trigonométricas secantes gama de Dominio y cosecante y Las funciones cosecante y secante están estrechamente ligados a seno y coseno, porque son los respectivos recíprocos. En referencia al plano de coordenadas, cosecante es r/y, y secante es r/X. El valor de r es la longitud de la hipotenusa de un…
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
Encuentre la imagen especular de una función de la trigonometría en un gráfico Cuando multiplicas una función trigonométrica de un número negativo, todos los valores de salida se invierten en la señal. Los valores positivos se vuelven negativos y los valores negativos se convierten en positivos. El efecto que esta…
Gráfico secante inversa y cosecante Las gráficas de las funciones cosecante secantes e inversas inversas tomarán un poco de explicación. En primer lugar, tener en cuenta que las funciones secante y cosecante no tienen valores de salida (y-valores) entre -1 y 1, por lo que un…
Múltiplos gráfica de la función tangente En trigonometría, valores tangentes van desde menos infinito hasta el infinito positivo. Así que cuando usted multiplica toda la función tangente de un número, esto es lo que sucede: Si se multiplica por un número mayor que 1, la función se…
Funciones Gráfico tangentes con multiplicadores variables En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…
Graficar las asíntotas de una función cotangente Las gráficas de la función tangente sientan las bases para las gráficas de la función cotangente. Después de todo, la tangente y cotangente son cofunciones y recíprocos, y tienen todo tipo de conexiones.Las gráficas de estas dos funciones son…
Grafica la función cosecante Una manera muy eficaz de graficar la función cosecante es hacer primero un boceto rápido de la función seno (su recíproco). Con el boceto de seno en su lugar, se puede dibujar las asíntotas de la función cosecante a través de la X-intercepta…
Grafica la asíntota de una función tangente Un asíntota es una línea que ayuda a dar sentido a una gráfica de una función trigonometría. Esta línea no es parte del ficos de la función sino que ayuda a determinar la forma de la curva, mostrando donde la curva tiende a ser una línea…
Graficar las asíntotas de una función secante Para graficar la curva de la secante, primero identificar las asíntotas determinando donde el recíproco de la secante - coseno - es igual a 0. Luego de realizar el boceto en ese recíproco, para que pueda determinar los puntos de inflexión y la…
Cómo reconocer los gráficos básicos trigonométricas Las gráficas de las funciones trigonométricas tienen muchas similitudes y muchas diferencias. Los gráficos del seno y el coseno parecen mucho, al igual que la tangente y cotangente, y luego la secante y cosecante tienen similitudes. Pero esos…