Cómo reconocer los gráficos básicos trigonométricas
Las gráficas de las funciones trigonométricas tienen muchas similitudes y muchas diferencias. Los gráficos del seno y el coseno parecen mucho, al igual que la tangente y cotangente, y luego la secante y cosecante tienen similitudes. Pero esos tres agrupaciones se ven diferentes uno del otro.
Conteúdo
La única característica que los une a todos es el hecho de que son periódica, lo que significa que repiten la misma curva o patrón una y otra vez, en cualquier dirección a lo largo del X-eje.
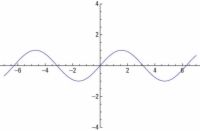  Agrandar1 La gráfica de y = Sen X.La gráfica de la función seno es una buena onda, continua que rueda junto con suavidad y sigue repitiéndose. El dominio o X-valores, de la función seno incluye todos los ángulos en grados o todos los números reales en radianes, por lo que la curva no tiene roturas o agujeros. | 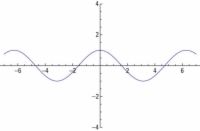 Agrandar2 La gráfica de y = Cos X.La relación entre las gráficas de seno y coseno es que el coseno es el mismo que el sine desplaza a la izquierda en 90 grados. | 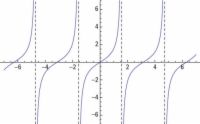 Agrandar3 La gráfica de y = Tan X.La función tangente se puede escribir como la relación de la sinusoidal dividido por el coseno. |
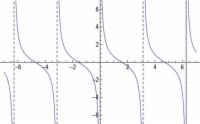 Agrandar4 La gráfica de y = Cot X.Las gráficas de la función tangente sientan las bases para las gráficas de la cotangente. Después de todo, son cofunciones y recíprocos, y tienen todo tipo de conexiones. | 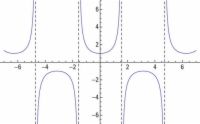 Agrandar5 La gráfica de y = Sec X.Las técnicas que se utilizan para representar gráficamente la curva de la secante paralelo los que se utiliza para representar gráficamente la cosecante. En primer lugar, identificar las asíntotas determinando donde el recíproco de la secante - coseno - es igual a 0. A continuación esbozar en esa reciprocidad, y se puede determinar los puntos de inflexión y la forma general de la gráfica secante. | 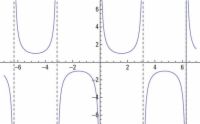 Agrandar6 La gráfica de y = Csc X.La función cosecante es el recíproco de la función seno (es decir, la cosecante es igual a 1 dividido por el seno). |
-
Representación gráfica de funciones trigonométricas en pre-cálculo -
Cómo calcular un ángulo usando funciones trigonométricas recíprocas -
Cómo calcular los valores para las seis funciones trigonométricas -
¿Cómo cambiar la amplitud, período, y la posición de un gráfico secante o cosecante -
Cómo graficar una función cosecante -
Cómo graficar una función secante
Cómo graficar una función tangente La función tangente tiene una gráfica de los padres al igual que cualquier otra función. Utilizando la gráfica de esta función, se puede hacer el mismo tipo de transformación que se aplica a la gráfica de los padres de cualquier función. La…
Cómo graficar seno, coseno y tangente Así, es necesario graficar un seno, coseno, tangente o función. Seno, coseno y tangente - y sus inversos, cosecante, secante y cotangente - son periódico funciones, lo que significa que sus gráficos contienen una forma básica que se repite una…
Cómo utilizar SOHCAHTOA para encontrar las funciones trigonométricas de un triángulo rectángulo El estudio de la trigonometría comienza con el triángulo rectángulo. Las tres funciones principales trigonométricas (seno, coseno y tangente) y sus inversos (cosecante, secante y cotangente) todo lo que dicen algo acerca de las longitudes de los…
Asignar funciones trigonométricas negativos y positivos por cuadrante Los valores de seno para 30, 150, 210 y 330 grados son 1/2, 1/2, -1/2 y -1/2, respectivamente. Todos estos múltiplos de 30 grados tienen un pecado cuyo valor absoluto del medio. La siguiente regla y figura ayudarle a determinar si un valor…
La comparación de funciones seno y coseno en un gráfico La relación entre el coseno y seno gráficos es que el coseno es el mismo que el sine - solamente se desplaza a la izquierda en 90 grados, o pi-/ 2. La ecuación de trigonometría que representa esta relación esMira las gráficas de las funciones…
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
Sine Express en términos de cotangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
Sine Express en términos de la tangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
Graficar una función seno usando amplitud La función seno y cualquiera de sus variaciones tienen dos características importantes: la amplitud y periodo de la curva. Puede determinar estas características examinado sea la gráfica de la función o su ecuación.los amplitud de la función…
Funciones Gráfico de seno y coseno inversa Las gráficas de las funciones trigonométricas inversas son relativamente singularidad por ejemplo, seno inverso y el coseno inversa son un poco brusca y desarticulada. Estos gráficos son importantes debido a su impacto visual. Especialmente en el…
Funciones Gráfico tangente inversa y cotangente Las gráficas de las funciones tangente y cotangente son muy interesantes porque implican dos asíntotas horizontales. Las asíntotas ayudan con las formas de las curvas y hacer hincapié en el hecho de que algunos ángulos no funcionarán con las…
Graficar las asíntotas de una función cotangente Las gráficas de la función tangente sientan las bases para las gráficas de la función cotangente. Después de todo, la tangente y cotangente son cofunciones y recíprocos, y tienen todo tipo de conexiones.Las gráficas de estas dos funciones son…