Graficar las asíntotas de una función cotangente
Las gráficas de la función tangente sientan las bases para las gráficas de la función cotangente. Después de todo, la tangente y cotangente son cofunciones y recíprocos, y tienen todo tipo de conexiones.
Las gráficas de estas dos funciones son similares en muchos aspectos: Ambos tienen asíntotas que cruzan la gráfica a intervalos regulares, los gráficos de ir de menos infinito a más infinito en valor, y son tanto afectados por la multiplicación y la adición. La mayor diferencia en los gráficos se encuentra en la dirección en la que se dibujan los gráficos. Los valores de la función tangente parecen subir a medida que lee de izquierda a derecha. La función va hacia arriba, desaparece de la gráfica, y luego vuelve a aparecer abajo para empezar todo de nuevo. La función cotangente hace lo contrario - que parece caer cuando se lee de izquierda a derecha.
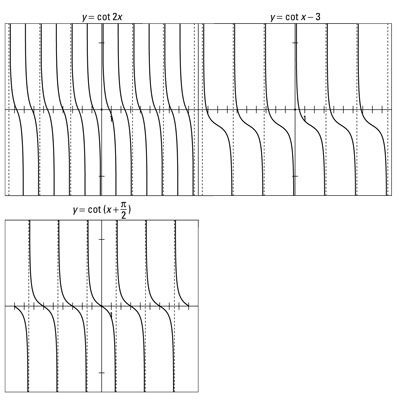
Las asíntotas de la curva cotangente ocurren donde la función seno es igual a 0, porque
Ecuaciones de las asíntotas son de la forma y = npi-, dónde n es un número entero. Algunos ejemplos de las asíntotas son y = -3pi-, y = -2pi-, y = -pi-, y = 0, y = pi-, y = 2pi-, y y = 3pi-. La siguiente figura muestra la función cotangente graficada entre -3pi- y 3pi-.
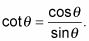
Al igual que las otras funciones, cotangente repite los mismos valores de una y otra. Puede aplicar los mismos tipos de variaciones de cotangente que usted puede a la tangente. La siguiente figura muestra tres ejemplos de variaciones: la multiplicación de la variable ángulo, restando de la función, y la adición a la variable ángulo.
¿Cómo simplificar una expresión utilizando identidades de función co- Si usted toma la gráfica de y = Sen X y desplazar hacia la izquierda por pi / 2 unidades, se ve exactamente como la gráfica de y = Cos X. Lo mismo es cierto para la tangente y cotangente, así como secante y cosecante. Esa es la premisa básica de…
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
Gama de funciones trigonométricas tangente y cotangente Dominio y La tangente y cotangente están relacionadas no sólo por el hecho de que son recíprocos, sino también por el comportamiento de sus rangos. En referencia al plano de coordenadas, tangente es y/X, y cotangente es X/y. Los dominios de ambas…
Sine Express en términos de cotangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
Funciones Gráfico tangente inversa y cotangente Las gráficas de las funciones tangente y cotangente son muy interesantes porque implican dos asíntotas horizontales. Las asíntotas ayudan con las formas de las curvas y hacer hincapié en el hecho de que algunos ángulos no funcionarán con las…
Múltiplos gráfica de la función tangente En trigonometría, valores tangentes van desde menos infinito hasta el infinito positivo. Así que cuando usted multiplica toda la función tangente de un número, esto es lo que sucede: Si se multiplica por un número mayor que 1, la función se…
Funciones Gráfico tangentes con multiplicadores variables En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…
Grafica la función cosecante Una manera muy eficaz de graficar la función cosecante es hacer primero un boceto rápido de la función seno (su recíproco). Con el boceto de seno en su lugar, se puede dibujar las asíntotas de la función cosecante a través de la X-intercepta…
Grafica la asíntota de una función tangente Un asíntota es una línea que ayuda a dar sentido a una gráfica de una función trigonometría. Esta línea no es parte del ficos de la función sino que ayuda a determinar la forma de la curva, mostrando donde la curva tiende a ser una línea…
Variaciones Gráfico en una función secante La gráfica de una función secante es diferente de la cosecante de varias maneras, pero una de las maneras más evidentes es que la gráfica de la secante es simétrica con respecto al y-eje. El secante es un espejo de reflexión sobre ese eje.…
Graficar las asíntotas de una función secante Para graficar la curva de la secante, primero identificar las asíntotas determinando donde el recíproco de la secante - coseno - es igual a 0. Luego de realizar el boceto en ese recíproco, para que pueda determinar los puntos de inflexión y la…
Cómo reconocer los gráficos básicos trigonométricas Las gráficas de las funciones trigonométricas tienen muchas similitudes y muchas diferencias. Los gráficos del seno y el coseno parecen mucho, al igual que la tangente y cotangente, y luego la secante y cosecante tienen similitudes. Pero esos…